Biết rằng Gy ⊥ Hz. Giá trị các góc như hình vẽ.
Số đo góc x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HB
0
T
20 tháng 11 2023
Xét \(\Delta FEH\) vuông tại \(F\) có:
\(\widehat{E}+\widehat{H}=90^\circ \) (định lí về tổng hai góc nhọn trong tam giác vuông)
\(\Rightarrow x+y=90^{\circ}\)
Lại có: \(x-y=18^{\circ}\)
\(\Rightarrow x+y-\left(x-y\right)=90^{\circ}-18^{\circ}\)
\(\Rightarrow x+y-x+y=72^{\circ}\)
\(\Rightarrow2y=72^{\circ}\)
\(\Rightarrow y=72^{\circ}:2=36^{\circ}\)
Khi đó: \(x-36^{\circ}=18^{\circ}\)
\(\Rightarrow x=18^{\circ}+36^{\circ}=54^{\circ}\)
Vậy: ...
b) 
b) 
; b) Chứng minh: OD 
AB
và x – y + z = – 49.
DV
0
HQ
Hà Quang Minh
Giáo viên
7 tháng 10 2023
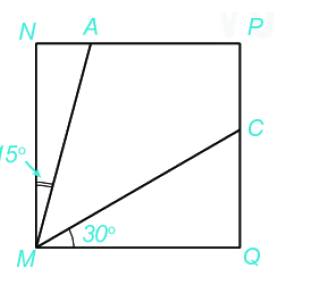
a, Các điểm nằm trong góc AMC là: điểm P.
b, \(\widehat {AMC} = 45^\circ \).
c, Ta có: \(\widehat{NMA}=15^0; \widehat{CMQ}=30^0; \widehat{AMC}=45^0\) nên \(\widehat{NMA}< \widehat{CMQ} < \widehat{AMC}\)
Vậy các góc theo thứ tự tăng dần là: \(\widehat{NMA}; \widehat{CMQ} ; \widehat{AMC}\)
22 tháng 8 2021
Vì Oz là tia phân giác của góc xOy
\(\Rightarrow\widehat{xOz}=\frac{\widehat{xOy}}{2}=\frac{120^o}{2}=60^o\)
Vì Ot là tia phân giác của góc xOz
\(\Rightarrow\widehat{xOt}=\frac{\widehat{xOz}}{2}=\frac{60^o}{2}=30^o\)