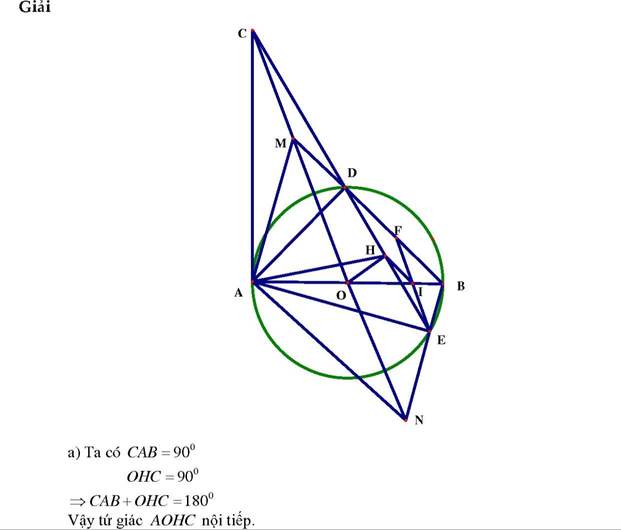
Cho đường tròn tâm O bán kính R , đường kính AB. Vẽ tiếp tuyến Ax , D thuộc Ax . Từ điểm D trên Ax kẻ tiếp tuyến DC với đường tròn. Từ C hạ đường vuông góc, CH xuống AB , đường thẳng BC cắt Ax tại E . CM:
a) D trung điểm AE
b) BD đi qua trung điểm CH

.png)