Tìm GTNN của P=2x2+y2-2xy-6x+2y+2024
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2


\(P=x^2+2y^2+2xy-6x-8y+2024\)
\(P=x^2+y^2+y^2+2xy-6x-6y-2y+2024\)
\(P=\left(x^2+2xy+y^2\right)-\left(6x+6y\right)+9+y^2-2y+1+2014\)
\(P=\left(x+y\right)^2-2\left(x+y\right)3+3^2+\left(y^2-2y+1\right)+2014\)
\(P=\left(x+y-3\right)^2+\left(y-1\right)^2+2014\)
\(P\ge2014\forall x;y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y-3=0\\y-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=1\end{cases}}}\)
Vậy.....

`A=2x^2-2xy-6x+y^2+10`
`A=x^2-2xy+y^2+x^2-6x+10`
`A=(x-y)^2+x^2-6x+9+1`
`A=(x-y)^2+(x-3)^2+1`
Vì `(x-y)^2+(x-3)^2>=0=>A>=1`
Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`


Lời giải:
$2x^2+y^2+2xy-6x-2y=8$
$\Leftrightarrow (x^2+y^2+2xy)+x^2-6x-2y=8$
$\Leftrightarrow (x+y)^2-2(x+y)+x^2-4x=8$
$\Leftrightarrow (x+y)^2-2(x+y)+1+(x^2-4x+4)=13$
$\Leftrightarrow (x+y-1)^2+(x-2)^2=13$
$\Rightarrow (x-2)^2=13-(x+y-1)^2\leq 13$
Mà $(x-2)^2$ là scp với mọi $x$ nguyên nên $(x-2)^2\in\left\{0; 1; 4; 9\right\}$
Nếu $(x-2)^2=0\Rightarrow (x+y-1)^2=13-(x-2)^2=13$ (không là scp - loại)
Nếu $(x-2)^2=1\Rightarrow (x+y-1)^2=12$ (không là scp - loại)
Nếu $(x-2)^2=4\Rightarrow (x+y-1)^2=9$
$\Rightarrow x-2=\pm 2$ và $x+y-1=\pm 3$
TH1: $x-2=2; x+y-1=3\Rightarrow x=4; y=0$
TH2: $x-2=2; x+y-1=-3\Rightarrow x=4; y=-6$
TH3: $x-2=-2; x+y-1=3\Rightarrow x=0; y=4$
TH4: $x-2=-2; x+y-1=-3\Rightarrow x=0; y=-2$
Nếu $(x-2)^=9\Rightarrow (x+y-1)^2=4$ (bạn cũng làm tương tự trên)

\(A=2x^2+y^2-2x+2xy+2y+3=y^2+2y\left(x+1\right)+\left(x+1\right)^2+\left(x^2-4x+4\right)-2=\left(y+x+1\right)^2+\left(x-2\right)^2-2\ge-2\)
\(minA=-2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)
\(P=x^3+2021xy+y^3\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+2021xy\)
\(=\left(\dfrac{2021}{3}\right)^3\)
\(=\dfrac{8254655261}{27}\)

A= 2x^2 + y^2 - 2xy -2x+3
A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2
A= (x-y)^2 + (x-1)^2 + 2
(x-y)^2> hoặc = 0 với mọi giá trị của x
(x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2
=> A lớn hơn hoặc bằng 2
=> GTNN của A=2 tại x=y=1
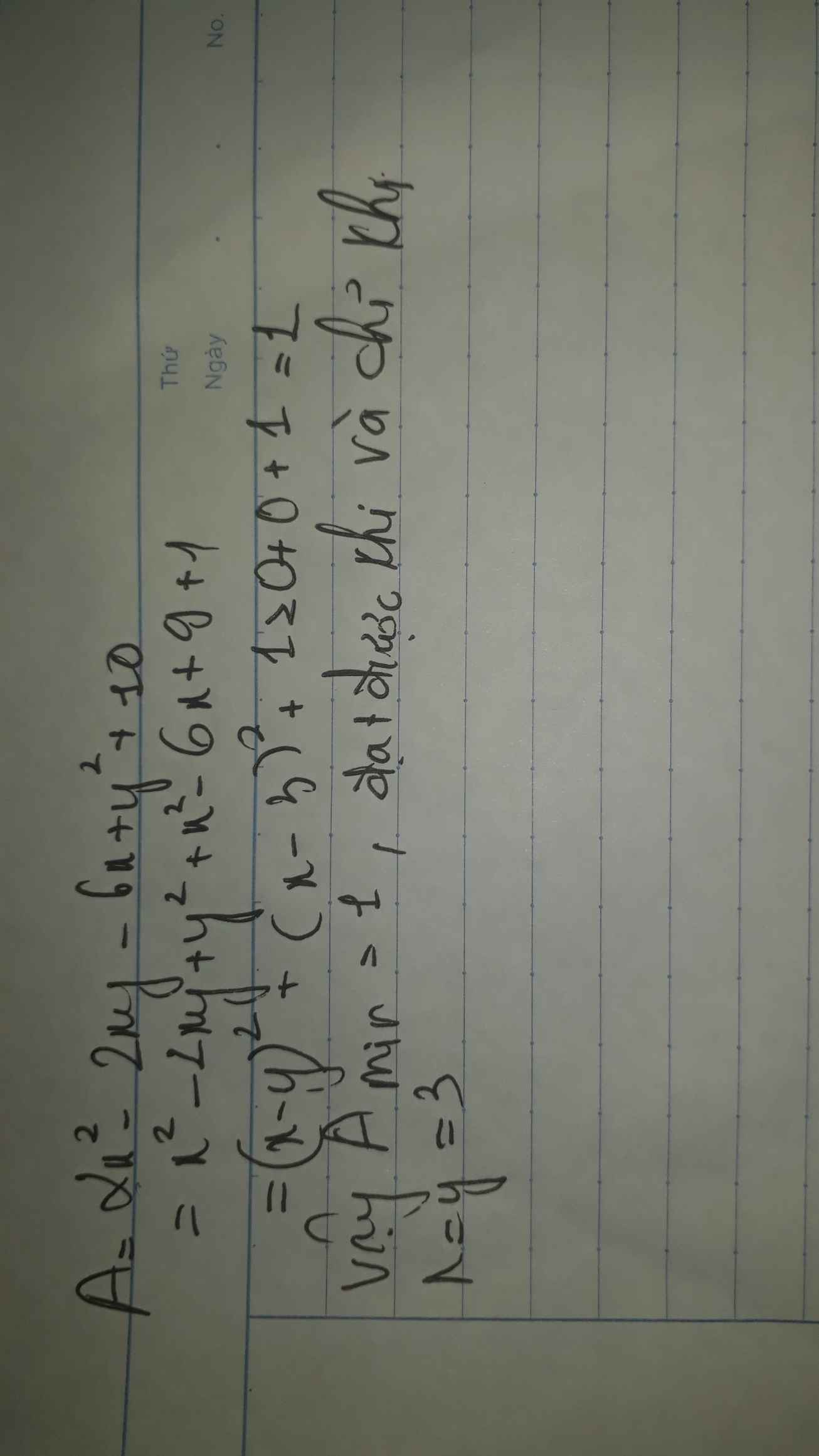
P=2x2+y2-2xy-6x+2y+2024
=>2P=4x2+2y2-4xy-12x+4y+4048
=(2x-y-3)2+y2-2y+1+4038
=(2x-y-3)2+(y-1)2+4038> hoặc = 4038
Dấu = xảy ra <=>2x-y-3=0 và y-1=0=>x=2;y=1=>2p=4038=>p=2019
Vậy Pmin=2019<=>x=2;y=1
Ta có:
P = 2x2 + y2 - 2xy - 6x + 2y + 2024
P = (x2 - 2xy + y2) - 2(x - y) + 1 + (x2 - 4x + 4) + 2019
P = [(x - y)2 - 2(x - y) + 1] + (x - 2)2 + 2019
P = (x - y - 1)2 + (x - 2)2 + 2019 \(\ge\)2019 \(\forall\)x;y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-y-1=0\\x-2=0\end{cases}}\) <=> \(\hept{\begin{cases}y=x-1\\x=2\end{cases}}\) <=> \(\hept{\begin{cases}y=1\\x=2\end{cases}}\)
Vậy MinP = 2019 <=> x = 2 và y = 1