Vẽ hình và ghi giả thiết, kết luận của định lí sau: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cung vuông góc với đường thẳng kia
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 8 2017
Vẽ hình thì dựa theo trong sách có nhé bạn!
a/ Bài a của bạn mình đọc không hiểu lắm hình như viết sai đề phải không bạn?
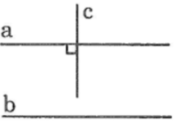
b/ GT: a song song với b,
c vuông góc với a
KL: c vuông góc với b
CẢM ƠN ĐÃ ĐỌC ĐÁP ÁN CỦA MÌNH
19 tháng 9 2023
Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b.
Thật vậy,
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \)nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)(đpcm)
12 tháng 10 2018
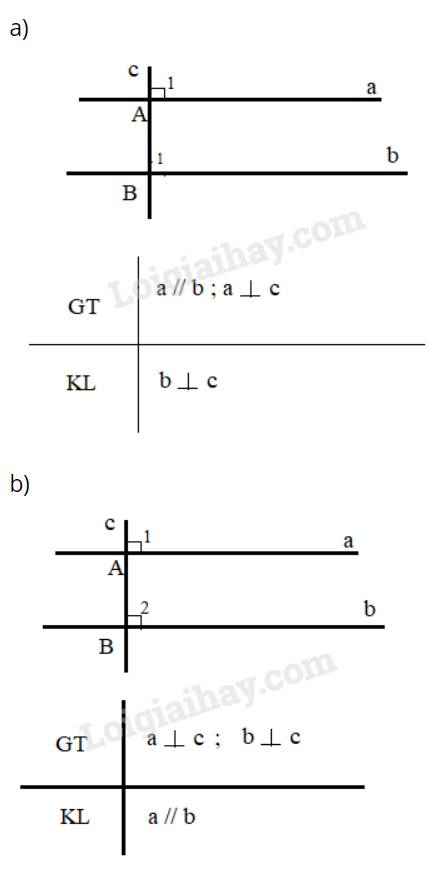
a) Giả thiết : Nếu 1 đường thẳng cắt 1 trong 2 dường thẳng song song
Kết luận: thì nó cắt đường thẳng kia
b) Giả thiết : Nếu 1 đường thẳng vuông góc với 1 trong hai đường thẳng song song
Kết luận : thì nó cũng vuông góc với đường thẳng kia
CHÚC BẠN HỌC TỐT NHA !
29 tháng 12 2023
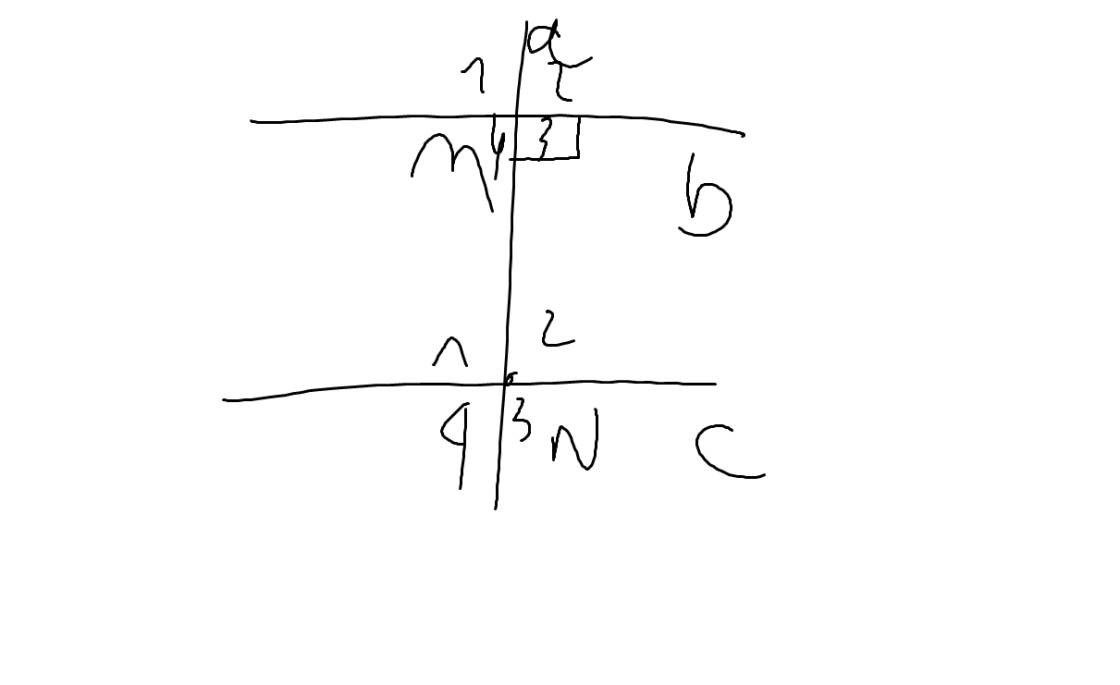
| GT | a\(\perp\)b tại M a cắt c tại N b//c |
| KL | a\(\perp\)c tại N |
Chứng minh định lí:
Ta có: b//c
=>\(\widehat{M_3}=\widehat{N_1}\)(hai góc so le trong)
mà \(\widehat{M_3}=90^0\)
nên \(\widehat{N_1}=90^0\)
=>a\(\perp\)c tại N
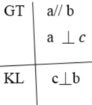
vẽ hình thì cậu tự vẽ nhé thì 2 đường thẳng song song gọi là a và b.Còn đường vuông góc gọi là c
GT:
KL: