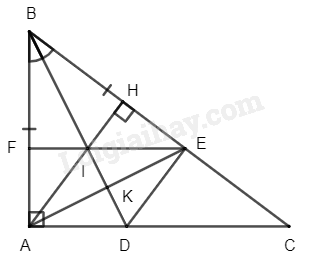
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:

\(BA = BE\) (gt)

\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)

\(BD\) chung

Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)

b) Vì \(\Delta ABD = \Delta EBD\) (cmt)

Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)

Suy ra \(DE \bot BC\)

Mà \(AH \bot BC\) (gt)

Suy ra \(AH\) // \(DE\)

Suy ra \(ADEH\) là hình thang

Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)

Suy ra \(ADEH\) là hình thang vuông

c) 

Gọi \(K\) là giao điểm của \(AE\) và \(AD\)

Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)

Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )

Suy ra \(BK\) cũng là đường cao

Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)

Suy ra \(I\) là trực tâm của \(\Delta ABE\)

Suy ra \(EF \bot AB\)

Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))

Suy ra \(AC\) // \(EF\)

Suy ra \(ACEF\) là hình thang

Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)

Suy ra \(ACEF\) là hình thang vuông

Câu a

Xét tam giác ABD và AMD có

AB = AM từ gt

Góc BAD = MAD vì AD phân giác BAM

AD chung

=> 2 tam guacs bằng nhau

Câu b

Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD

Bd = bm vì 2 tam giác ở câu a bằng nhau

Góc BDE bằng MDC đối đỉnh

=> 2 tam giác bằng nhau

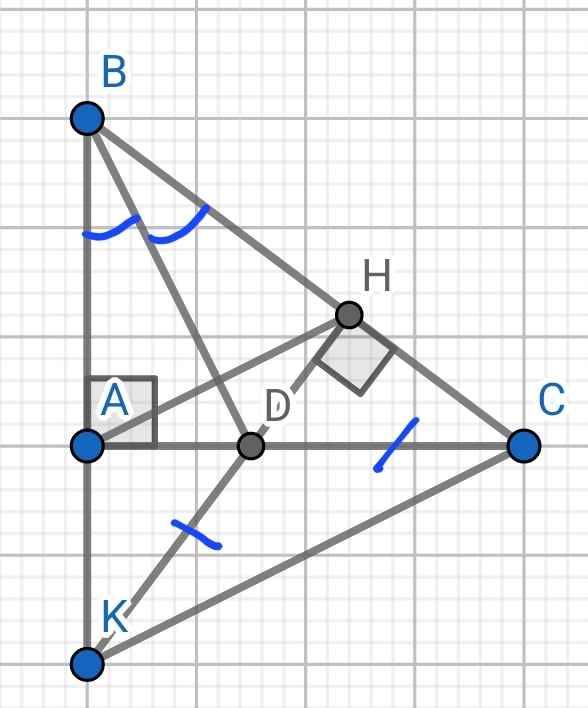
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:

BD chung

∠ABD = ∠HBD (BD là phân giác của ∠ABH)

⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)

b) Do ∆ABD = ∆HBD (cmt)

⇒ AB = BH (hai cạnh tương ứng)

⇒ B nằm trên đường trung trực của AH (1)

Do ∆ABD = ∆HBD (cmt)

⇒ AD = HD (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AH (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AH

c) Xét ∆ADK và ∆HDC có:

AD = HD (cmt)

∠ADK = ∠HDC (đối đỉnh)

DK = DC (gt)

⇒ ∆ADK = ∆HDC (c-g-c)

⇒ ∠DAK = ∠DHC (hai góc tương ứng)

⇒ ∠DAK = 90⁰

Mà ∠DAB = 90⁰

⇒ ∠DAK + ∠DAB = 180⁰

⇒ B, A, K thẳng hàng

a: Ta có: \(\widehat{BMA}+\widehat{ABM}=90^0\)

\(\widehat{BMD}+\widehat{DBM}=90^0\)

mà \(\widehat{ABM}=\widehat{DBM}\)

nên \(\widehat{BMA}=\widehat{BMD}\)

c: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có 

BM chung

\(\widehat{ABM}=\widehat{DBM}\)

Do đó: ΔBAM=ΔBDM

Suy ra: MA=MD

Xét ΔAME vuông tại A và ΔDMC vuông tại D có 

MA=MD

\(\widehat{AME}=\widehat{DMC}\)

Do đó: ΔAME=ΔDMC

a: Xét ΔABD và ΔKBD có 

BA=BK

\(\widehat{ABD}=\widehat{KBD}\)

BD chung

Do đó: ΔBAD=ΔBKD

Sau gần một buổi trưa lăn lội với Thales, đồng dạng ở câu b thì t đã nghĩ đến cách của lớp 7 ~ ai dè làm được ^^

vaidaibangioithe))):