Nung hỗn hợp X gồm: Al và Fe2O3 được hỗn hợp Y. Hoà tan Y bằng dung dịch NaOH dư thu được dung dịch Z và 11,2 gam chất rắn E duy nhất, đồng thời trong quá trình phản ứng không có khí bay ra. Tính thành phần % theo khối lượng từng chất trong hỗn hợp X. Biết các phản ứng xảy ra hoàn toàn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2019
Giải thích:
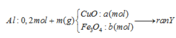
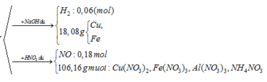
Coi trong mỗi phần có 0,2 mol Al
- Rắn Y + NaOH → 0,06 nH2
BT: e => nAl DƯ = 2/3 nH2 = 2/3. 0,06 = 0,04 ( mol)
BTNT: Al => nAl2O3 = ½ ( nAlbđ – nAl dư) = ½ ( 0,2 – 0,04) = 0,08 (mol)
BTKL: m = mFe, Cu + mO = 18,08 + 0,08.3.16 = 21,92 (g)
=> 80a + 232b = 21,92 (1)
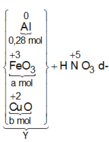
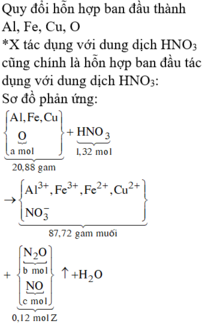
- Rắn Y + HNO3
Sau tất cả quá trình ta có: Al → Al+3 ; Fe+8/3 → Fe+3, N+5 → N+2; N+5→ N-3
BT e ta có: 3nAl + nFe3O4 = 3nNO + 8nNH4NO3
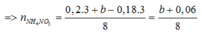
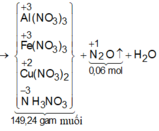
mmuối = mAl(NO3)3 + mCu(NO3)3 + mFe(NO3)3 + mNH4NO3
=>213.0,2 +188a + 242.3b + 80 ( b+0,06)/8 = 106,12 (2)
Từ (1) và (2) => a = 0,1 và b = 0,06
=> mFe3O4 = 232.2b = 232.2.0,1= 27,84 (g) ( Vì hỗn hợp ban đầu nên phải nhân đôi số liệu)
Đáp án A
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 2 2022
Gọi số mol Al, Fe2O3 mỗi phần lần lượt là a,b (mol) (a,b>0)
- Xét phần 2:
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{H_2\left(P2\right)}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\\ n_{Al\left(P2\right)}=\dfrac{2}{3}.0,2=\dfrac{2}{15}\left(mol\right)\\ m_{Al\left(P2\right)}=\dfrac{2}{15}.27=1,8\left(g\right)\\ m_{P2}=\dfrac{40,1}{2}=20,05\left(g\right)\\ \%m_{\dfrac{Al\left(P2\right)}{P_2}}=\%m_{\dfrac{Al}{2Phần}}=\dfrac{1,8}{20,05}.100\approx8,978\%\)
16 tháng 2 2022
P1: Do chất rắn tác dụng với NaOH có khí thoát ra
=> trong Y chứa Al
P2: Gọi (nAl; nFe; nAl2O3) = (a;b;c)
PTHH: 2Al + 6HCl --> 2AlCl3 + 3H2
a---------------------->1,5a
Fe + 2HCl --> FeCl2 + H2
b---------------------->b
=> 1,5a + b = \(\dfrac{4,48}{22,4}=0,2\left(mol\right)\) (1)
mY = mX = 40,1
=> 54a + 112b + 204c = 40,1 (2)
PTHH: 2Al + Fe2O3 --to--> Al2O3 + 2Fe
=> \(\dfrac{n_{Fe}}{n_{Al_2O_3}}=\dfrac{2}{1}\) => \(\dfrac{b}{c}=\dfrac{2}{1}\) (3)
(1)(2)(3) => \(\left\{{}\begin{matrix}a=\dfrac{9}{890}\left(mol\right)\\b=\dfrac{329}{1780}\left(mol\right)\\c=\dfrac{329}{3560}\left(mol\right)\end{matrix}\right.\)
=> nAl = 2.(a + 2c) = \(\dfrac{347}{890}\left(mol\right)\)
=> \(\%Al=\dfrac{27.\dfrac{347}{890}}{40,1}.100\%=26,252\%\)
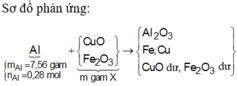
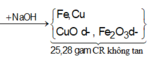
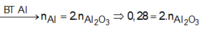
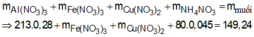
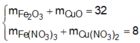
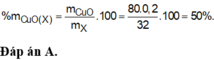
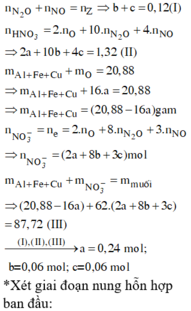
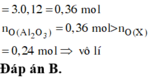
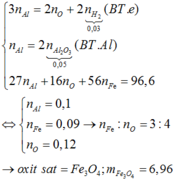
$n_{Fe} = \dfrac{11,2}{56} = 0,2(mol)
\(2Al+Fe_2O_3\xrightarrow[]{t^o}2Fe+Al_2O_3\)
0,2 0,1 0,2 (mol)
$\%m_{Al} = \dfrac{0,2.27}{0,2.27 + 0,1.160}.100\% = 25,23\%$
$\%m_{Fe_2O_3} = 100\% -25,23\% = 74,77\%$