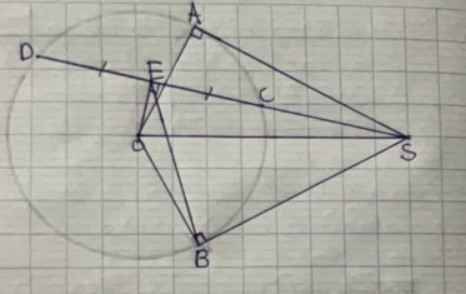
Cho đường tròn (o,r) và một điểm Hcố định nằm ngoài đường tròn.Qua H kẻ đường thẳng d vuông góc với đoạn thẳng OH. Từ một điểm S bất kỳ
Trên đường thẳng d kẻ hai tiếp tuyến SA SB với đường tròn (o,r) (A,B là tiếp điểm). Gọi M,N lần lượt là giao điểm của đoạn thẳng SO với đoạn thẳng AB và với đường tròn (o,r)
a) chứng minh 4 điểm S,AO,B cùng nằm trên một đường tròn
b) chứng minh OM Os = R bình