\(Cho\) \(\Delta ABC,\) \(kẻ\) \(BD\perp AC\) .\(Kẻ\) \(CE\perp AB.\) \(Trên\) \(tia\) \(đối\) \(của\) \(tia\) \(BD,\) \(lấy\) \(H\) \(sao\) \(cho\) \(BH=AC.\) \(Trên\) \(tia\) \(đối\) \(của\) \(tia\) \(CE,\) \(lấy\) \(điểm\) \(K\) \(sao\) \(cho\) \(CK=AB.\)...
Đọc tiếp
\(Cho\) \(\Delta ABC,\) \(kẻ\) \(BD\perp AC\) .\(Kẻ\) \(CE\perp AB.\) \(Trên\) \(tia\) \(đối\) \(của\) \(tia\) \(BD,\) \(lấy\) \(H\) \(sao\) \(cho\) \(BH=AC.\) \(Trên\) \(tia\) \(đối\) \(của\) \(tia\) \(CE,\) \(lấy\) \(điểm\) \(K\) \(sao\) \(cho\) \(CK=AB.\) \(C.m:\)
\(a)\widehat{ABD}=\widehat{ACE}\)
\(b)AH=AK\)
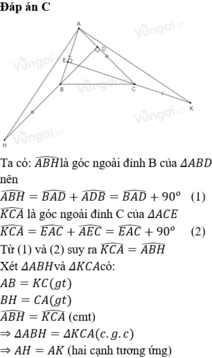
a) Ta có:
\(\widehat{ACK}=\widehat{A}+\widehat{AEC}\) ( tính chất góc ngoài của tam giác ).
=> \(\widehat{ACK}=\widehat{A}+90^0\) (1).
\(\widehat{ABH}=\widehat{A}+\widehat{ADB}\) ( tính chất góc ngoài của tam giác ).
=> \(\widehat{ABH}=\widehat{A}+90^0\) (2).
Từ (1) và (2) => \(\widehat{ABH}=\widehat{ACK}.\)
Hay \(\widehat{ABD}=\widehat{ACE}.\)
b) Xét 2 \(\Delta\) \(ABH\) và \(KCA\) có:
\(BH=CA\left(gt\right)\)
\(\widehat{ABH}=\widehat{ACK}\left(cmt\right)\)
\(AB=CK\left(gt\right)\)
=> \(\Delta ABH=\Delta KCA\left(c-g-c\right)\)
=> \(AH=AK\) (2 cạnh tương ứng) (đpcm).
Chúc bạn học tốt!