Cho tứ giác ABCD có hai đường chéo AC vuông góc với BD. Chứng minh rằng:
AB2 + CD2 = AD2 + BC2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

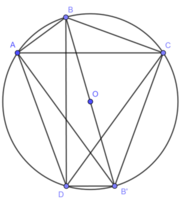
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: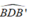 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do 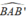 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)

a: Xet ΔAHB vuông ạti H và ΔDAB vuông tại A có
góc DBA chung
=>ΔAHB đồng dạng với ΔDAB
b: ΔABD vuông tại A có AH vuông góc BD
nên AD^2=DH*BD=DH*AC

Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB(Hai cạnh đối của hình bình hành ABCD)
\(\widehat{D}=\widehat{B}\)(Hai góc đối của hình bình hành ABCD)
Do đó: ΔAED=ΔCFB(cạnh huyền-góc nhọn)
Suy ra: AE=CF(Hai cạnh tương ứng) và ED=FB(hai cạnh tương ứng)
Ta có: ED+EC=DC(E nằm giữa D và C)
FB+FA=AB(F nằm giữa A và B)
mà AB=DC(Hai cạnh đối của hình bình hành ABCD)
và ED=FB(cmt)
nên EC=FA
Xét tứ giác ECFA có
EC=FA(cmt)
EA=CF(cmt)
Do đó: ECFA là hình bình hành(Dấu hiệu nhận biết hình bình hành)

a/ Xét tam giác AHD và tam giác BCH có:
góc AHD = góc BHC = 90 độ (gt)
góc DAH = góc DBC (hai góc = nhau cùng nhìn cạnh DC, tứ giác ABCD nội tiếp)
=> tam giác AHD đồng dạng tam giác BHC (g.g)
=> HA/HB = HD/HC
=> HA.HC = HB.HD

Giả sử AB ⊥ CD ta phải chứng minh:
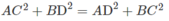
Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
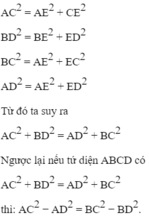
Nếu
A
C
2
−
A
D
2
=
B
C
2
−
B
D
2
=
k
2
thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho 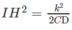
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.
Nếu A C 2 − A D 2 = B C 2 − B D 2 = - k 2 thì ta có và đưa về trường hợp xét như trên A C 2 − A D 2 = B C 2 − B D 2 = - k 2 .
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi A B 2 + C D 2 = A C 2 + B C 2 .

Xét ΔABO vuông tại O và ΔDCO vuông tại O có
góc BAO=góc CDO
=>ΔABO đồng dạng với ΔDCO
Xét ΔBCO vuông tại O và ΔADO vuông tại O có
góc OBC=góc OAD
=>ΔBCO đồng dạng với ΔADO