Cho đường tròn (O) bán kính OA=R, dây MN vuông góc với OA tại trung điểm I của OA. Hai tiếp tuyến với đường tròn tại m và N cắt nhau tại B.
b/ CM: IO.NB=IM.NO
c/ Tính độ dài BM teo R. Tính diện tích tứ giác OMNB theo R.
d/ Kẻ đường kính NC của (O), E là giao điểm của MN và CB. CM : CM√EN=NC\(\sqrt{EM}\)

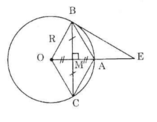
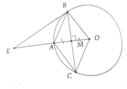
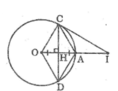

a/ Ta có
\(AO\perp MN\)
Nối BO \(\Rightarrow BO\perp MN;IM=IN\) (Hai tiếp tuyến cùng xuất phát từ 1 điểm ngoài đường tròn thì đường nối điểm đó với tâm vuông góc với dây cung nối 2 tiếp điểm tại trung điểm của dây cung đó)
\(\Rightarrow AO\equiv BO\) Hay nói cách khác B; A; I; O thẳng hàng
Xét hai tg vuông IMO và tg vuông NBO có
\(OM=ON=R\Rightarrow\Delta OMN\) cân tại O
\(OI\perp MN\)
\(\Rightarrow\widehat{MOI}=\widehat{BON}\) (trong tg cân đường cao từ đỉnh tg cân đồng thời là đường phân giác)
=> tg IMO đồng dạng với tg NBO \(\Rightarrow\frac{IO}{NO}=\frac{IM}{NB}\Rightarrow IO.NB=IM.NO\left(dpcm\right)\)
b/ Xét tg OMNB có
\(IM=IN;IO=IA\) => OMAN là hình bình hành \(\Rightarrow AM=ON=OM=AN=OA=R\)
=> tg AMO là tg đều mà \(MI\perp AO\Rightarrow\widehat{AMI}=\widehat{OMI}=30^o\) (Trong tg đều đường cao đồng thời là đường phân giác)
Xét tg vuông MIO có \(IO=\frac{MO}{2}=\frac{R}{2}\) (Trong tg vuông cạnh đối diện với góc \(30^o\) bằng nửa cạnh huyền)
Xét tg vuông BMO có
\(MO^2=OI.OB\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow OB=\frac{MO^2}{IO}=\frac{R^2}{\frac{R}{2}}=2R\)
Xét 2 tg vuông BMO và BNO có
BO chung
\(\widehat{MOI}=\widehat{BON}\left(cmt\right)\Rightarrow\Delta BMO=\Delta BNO\) (Theo trường hợp 2 tg vuông có cạnh huyền và 1 góc nhọn tương ứng bằng nhau thì bằng nhau)
\(\Rightarrow S_{OMNB}=S_{BMO}+S_{BNO}=2S_{BMO}=\frac{2.BM.MO}{2}=BM.MO=2R.R=2R^2\)
c/ Xét hình bình hành OMAN có \(MN\perp OA\) => OMAN là hình thoi (Hình bh có hai đường chéo vuông góc với nhau)
=> MN là đường phân giác của \(\widehat{AMO}\) và \(\widehat{ANO}\)
Mà \(\widehat{ANO}=\widehat{AMO}=60^o\) (Trong hbh hai góc đối diện bằng nhau) \(\Rightarrow\widehat{MNC}=30^o\)
Xét tg MNC có \(\widehat{NMC}=90^o\) (Góc nội tiếp chắn nửa đường tròn) => tg NMC là tg vuông tại M
\(\Rightarrow MC=\frac{NC}{2}=R\) (Trong tg vuông cạnh đối diện với góc \(30^o\) bằng nửa cạnh huyền
Ta có \(BI=BO-IO=2R-\frac{R}{2}=\frac{3R}{2}\)
Xét tg vuông ECM và tg vuông EBI có
MC//BI (cùng vuông góc với MN) \(\Rightarrow\widehat{MCE}=\widehat{IBE}\) (góc so le trong)
=> tg ECM đồng dạng tg EBI \(\Rightarrow\frac{MC}{BI}=\frac{EM}{EI}=\frac{R}{\frac{3R}{2}}=\frac{2}{3}\Rightarrow\frac{EM}{IM}=\frac{2}{5}\)
Xét tg vuông MNC có \(MN=\sqrt{NC^2-MC^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)
Mà \(IM=IN=\frac{MN}{2}=\frac{R\sqrt{3}}{2}\)
\(\Rightarrow\frac{EM}{IM}=\frac{EM}{\frac{R\sqrt{3}}{2}}=\frac{2}{5}\Rightarrow EM=\frac{R\sqrt{3}}{5}\)
Ta có \(EN=MN-EM=R\sqrt{3}-\frac{R\sqrt{3}}{5}=\frac{4R\sqrt{3}}{5}\)
\(\Rightarrow\frac{EN}{EM}=\frac{\frac{4R\sqrt{3}}{5}}{\frac{R\sqrt{3}}{5}}=4\Rightarrow\sqrt{\frac{EN}{EM}}=2\)
Mà đề bài bắt CM \(\sqrt{EN}=NC\sqrt{EM}\Rightarrow NC=\sqrt{\frac{EN}{EM}}\)
Mà NC=2R
Vậy xem lại đề bài
Sorry
\(\frac{NC}{CM}=\sqrt{\frac{EN}{EM}}\)
Mà \(\frac{NC}{CM}=\frac{2R}{R}=2\)
\(\Rightarrow\frac{NC}{CM}=\sqrt{\frac{EN}{EM}}\Rightarrow CM\sqrt{EN}=NC\sqrt{EM}\)