1 phần câu hỏi tự luạn của trường mình năm nay của bộ giáo dục
S = 4^0 + 4^1 + 4^2 + 4^3 + ... + 4^35
so sánh 3S với 64^12
1 xe tãi cứ 12 phút thì có 1 chuyến đi 1 xen buýt cứ 15 phút thì có 1 chuyến lúc 6 giờ sáng thì 2 xe giời bến cùng lúc hỏi đến lúc mấy giờ 2 xe cùng giời bến 1 lúc trong lần tiếp theo
mình chỉ nhớ 2 bài này thôi
kiểm tra học kì 1 môn toán trường THCS cẩm yên ( của phòng giáo dục huyện thạch thát )

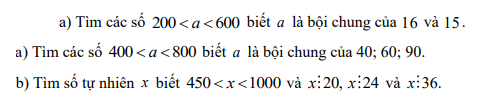
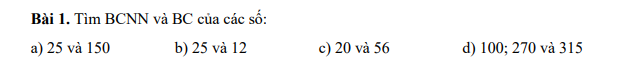
Đáp án câu 1: Câu hỏi của lam hue my - Toán lớp 6 - Học toán với OnlineMath
Sửa lại đề câu 2: Tại một bến xe, Cứ 12 phút thì có 1 xe tải rời bến. Cứ 15 phút thì có 1 xe buýt rời bến. Lúc 6 giờ sáng, hai xe rời bến cùng lúc. Hỏi đến lúc mấy giờ thì 2 xe cùng rời bến trong lần tiếp theo.
Giải:
Gọi a là khoảng thời gian từ lúc hai xe rời bến lần đầu đến lúc hai xe cùng rời bến lần tiếp theo. ( a> 0; phút )
Cứ 12 phút thì có 1 xe tải rời bến => a \(⋮\)12
Cứ 15 phút thì có 1 xe buýt rời bến => a \(⋮\)15
=> a\(\in\)BC( 12; 15)
Lại có a nhỏ nhất => a = BCNN ( 12; 15)
Có: 12 = 2\(^2\).3 ; 15 = 3. 5
=> a = 4.3.5 = 60 phút = 1 giờ
=> Lúc 7 giờ sáng 2 xe sẽ cùng rời bến.