cho hàm số y=x^2-2x-3. Dựa vào đồ thị hãy biện luận theo m số nghiệm của phương trình -2x^2+4x+2m-1=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:
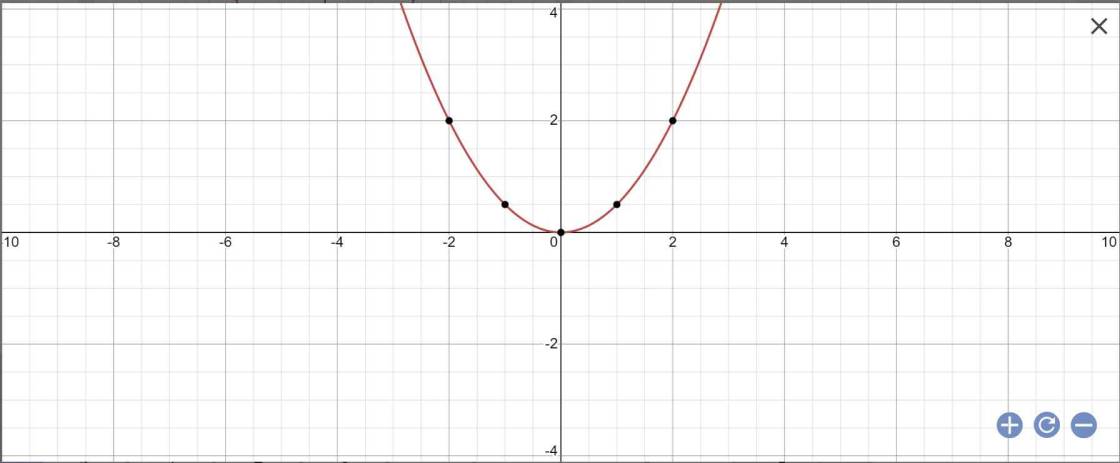
b: \(\Delta=\left(-2m\right)^2-4\cdot1\cdot4=4m^2-16\)
Để phương trình có hai nghiệm phân biệt thì 4m^2-16>0
=>m>2 hoặc m<-2
Để phương trình có nghiệm duy nhất thì 4m^2-16=0
=>m=2 hoặc m=-2
Để phương trìh vô nghiệm thì 4m^2-16<0
=>-2<m<2

a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |

\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
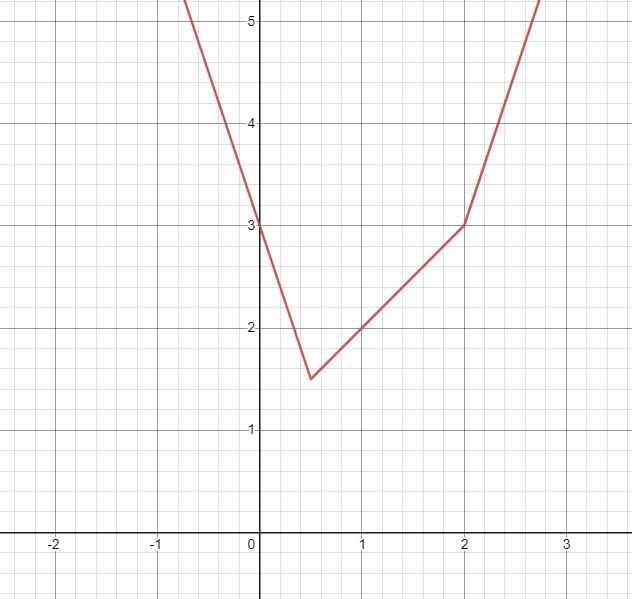
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)