a: 

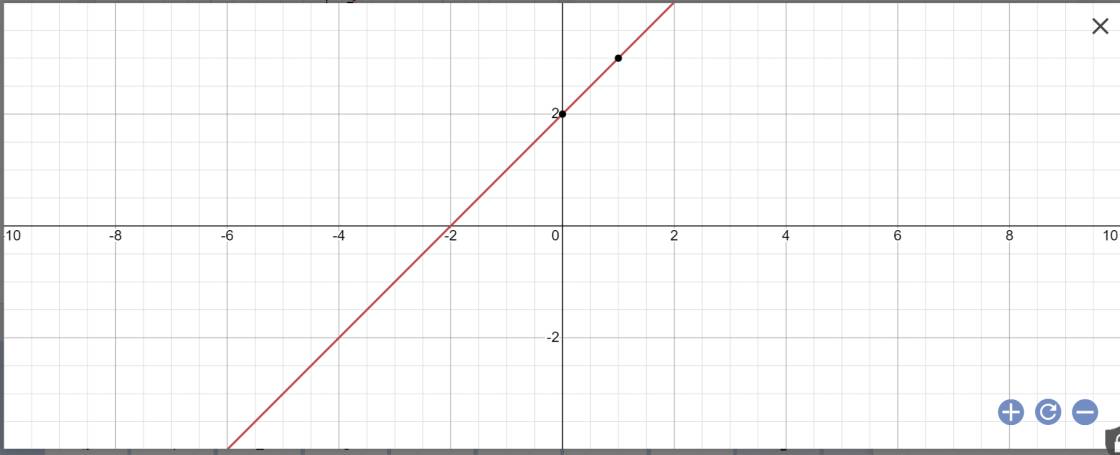
b:

Sửa đề: Tính diện tích tam giác ABO

tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)

Vậy: A(-2;0)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+2=2\end{matrix}\right.\)

Vậy: B(0;2)

O(0;0) A(-2;0); B(0;2)

\(OA=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{4}=2\)

\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{4}=2\)

\(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)

Vì \(OA^2+OB^2=AB^2\)

nên ΔOAB vuông tại O

=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)

c: Sửa đề: Tính góc tạo bởi đường thẳng với trục ox

Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox

\(tan\alpha=a=1\)

=>\(\alpha=45^0\)

Nè.Anh có kết bạn với em hông?

Rồi bạn Nguyễn Thị Thanh Mai 

\(b,\text{PT hoành độ giao điểm: }2x=-2x+4\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\)

làm ơn ai làm nhanh hộ mình với hãy giúp mik 

a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì

Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:

\(a\cdot4^2=4\)

\(\Leftrightarrow a\cdot16=4\)

hay \(a=\dfrac{1}{4}\)

a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)

\(\Rightarrow a=\dfrac{1}{4}\)

b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)

- Ta có đồ thì của hai hàm số :

c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)

\(\Leftrightarrow x^2+2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)

Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)

b: Vì (d')//(d) nên a=2

Vậy: (d'): y=2x+b

Thay x=1 và y=4 vào (d'), ta được:

b+2=4

hay b=2

cảm ơn nhiều ạ

a: Thay x=-2 vào y=-3x+4, ta được:

y=6+4=10

Thay x=-2 và y=10 vào hàm số \(y=ax^2\), ta được:

\(4a=10\)

hay a=5/2

c: (P): y=5/2x²

(d): y=-3x+4

Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}\dfrac{5}{2}x^2+3x-4=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x^2+6x-8=0\\y=-3x+4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x^2+10x-4x-8=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(5x-4\right)=0\\y=-3x+4\end{matrix}\right.\)

\(\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;10\right);\left(\dfrac{4}{5};\dfrac{8}{5}\right)\right\}\)

1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)

    b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5

       Thay y=5 và x=0 vào hs và tìm k

2. a) Tự vẽ

    b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)

    c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y)  (x=-2; y=0)

3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)

       Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1

        Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3