Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của BC và AC. Gọi D là điểm đối xứng với M qua N.
a) Cm MD//AB và tứ giác ABMD là hình bình hành.
b) Gọi E là điểm đối xứng với M qua AB. Cm A là trung điểm của đoạn DE.
c) Tìm điều kiện của tam giác ABM để tứ giác ABMD là hình thoi.
Chắc chắn sẽ tick cho bạn nào làm nhanh nhất >__< ~

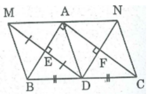
bài này mình chưa học nhưng nó tương tự như bài này dưới đây mình đã học
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có: HB = HD, GD = GC (gt)
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
a) EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC
b) EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC
c) EFGH là hình vuông ⇔ AD ⊥ BC và AD = BC