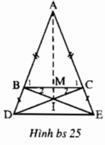
Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.

• doandieungoc
• 30/06/2020

Đáp án: 

Giải thích các bước giải: 

Xét ΔACD và ΔACDcó:

Góc DCE là góc ngoài đỉnh C của tam giác ấy, nên:

DCE^>CDA^

DCE^>CDA^

Hai tam giác BCD và EDC có hai cạnh bằng nhau từng đôi một

BD = EC (theo giả thiết)

CD là cạnh chung

Hai góc xen giữa hai cạnh ấy không bằng nhau

DCE^ >^CDB

DCE^>CDB^ 

=> hai cạnh đối diện với hai góc ấy không bằng nhau.

Ta suy ra: BC < DE.

Cop mạng lộ liễu thế

tam giác ABC cân tại A-->góc ABC=góc ACB (đ/lí tam giác cân)

góc ACE+góc ACB=180 độ (kề bù)

góc ABD+góc ABC=180 độ (kề bù)

mà góc ABC=góc ACB (cmt)

-->góc ACE=góc ABD (bắc cầu)

xét tam giác ABD và tam giác ACE có:

+AB=AC(gt)

+BD=CE(gt)

+góc ABD=góc ACE(cmt)

vậy tam giác ABD=tam giác ACE(cgc)

suy ra AD=AE

AD=AE(cmt)-->tam giác ADE cân tại A

thank you!Thanks for ticking me! I didn't expect I was right, I also think you will tick later like everyone else! I didn't expect you to tick early>))

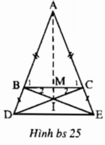
Xét ΔABM và ΔACM có:

AB = AC ( giả thiết)

BM = CM ( vì M là trung điểm BC )

AM chung

⇒ ΔABM = ΔACM (c.c.c)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180o

⇒ ∠AMB = ∠AMC = 90o hay AM ⊥ BC

Chứng minh tương tự ta có: IM ⊥ BC

⇒ A, I, M thẳng hàng (Qua 1 điểm ta kẻ được duy nhất 1 đường thẳng vuông góc với đường thẳng cho trước)

Hình vẽ đây em nhé. Sửa lại câu hỏi không có nói chứng minh gì nên a không giải được đâu nhé

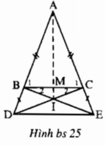
+)Theo giả thiết ta có: AB = AC và BD = CE nên:

AB + BD = AC + CE hay AD = AE.

+) Xét ΔABE và ΔACD có:

AB = AC (gt)

∠A chung

AE = AD (chứng minh trên)

⇒ ΔABE = ΔACD (c.g.c)

⇒ BE = CD (2 cạnh tương ứng) (1)

và ∠ABE = ∠ACD (2 góc tương ứng) (2)

Tam giác ABC cân nên ∠B1 = ∠C1. (3)

Từ (2) và (3) ⇒ ∠ABE - ∠B1 = ∠ACD - ∠C1, tức là ∠B2 = ∠C2.

⇒ ΔBIC cân tại I ⇒ IB = IC. (4)

Từ (1) và (4) suy ra BE - IB = CD – IC, tức là IE = ID.