Chọn chiều chuyển động của người là chiều dương. Hệ vật gồm thuyền và người. Do không có ma sát và tổng các ngoại lực tác dụng lên hệ vật (trọng lực và phản lực pháp tuyến) cân bằng nhau theo phương đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn.

Lúc đầu, hệ vật đứng yên đối với mặt hồ phẳng lặng ( v 0  = 0), nên tổng động lượng của nó có trị đại số bằng : p 0 = (M + m) v 0  = 0.

Khi người chạy với vận tốc v = 0,5 m/s đối với thuyền, thì tổng động lượng của hệ vật bằng : p = MV + m(v + V).

Áp dụng định luật bảo toàn động lượng :

p =  p 0  ⇒ MV + m(v + V) =0

suy ra vận tốc của thuyền : V = -mv/(M + m) = -50.0,5/(450 + 50) = -0,05(m/s)

Dấu trừ chứng tỏ vận tốc của thuyền ngược hướng với vận tốc của người.

Chọn chiều chuyển động của người là chiều dương. Hệ vật gồm thuyền và người. Do không có ma sát và tổng các ngoại lực tác dụng lên hệ vật (trọng lực và phản lực pháp tuyến) cân bằng nhau theo phương đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn.

Lúc đầu, hệ vật đứng yên đối với mặt hồ phẳng lặng ( v 0  = 0), nên tổng động lượng của nó có trị đại số bằng :  p 0  = (M + m) v 0  = 0.

Khi người chạy với vận tốc v = 0,5 m/s đối với mặt hồ, thì tổng động lượng của hệ vật có trị đại số bằng : p = M.v + m.v.

Áp dụng định luật bảo toàn động lượng : p =  p 0 ⇒ MV + mv = 0

suy ra vận tốc của thuyền : V = -mv/M = -50.0,5/450 ≈ 0,056(m/s)

Dấu trừ chứng tỏ vận tốc của thuyền ngược hướng với vận tốc của người

Ban đầu động lượng của hệ thuyền+ người bằng 0
Khi người đi từ mũi đến lái thì động lượng của người bằng  \(\overrightarrow{p_1}=m\overrightarrow{v_1}\)  ( với \(\overrightarrow{v_1}\) là vận tốc của người đối với bờ sông), còn thuyền sẽ có động lượng \(\overrightarrow{p_2}=M\overrightarrow{v_2}\) với \(\overrightarrow{v_2}\) là vận tốc của thuyền đối với bờ.
Theo phương ngang hệ không chịu tác dụng của ngoại lực ( do bỏ qua ma sát) nên động lượng của hệ được bảo toàn: \(\overrightarrow{0}=\overrightarrow{p_1}+\overrightarrow{p_2}=m\overrightarrow{v_1}+M\overrightarrow{v_2}\)

Suy ra: \(\overrightarrow{v_2}=-\frac{m}{M}m\overrightarrow{v_1}\left(1\right)\)

thuyền chuyển động ngược chiều với người.
Chọn chiều dương là chiều chuyển động của người và kí hiệu \(\overrightarrow{v_0}\) là vận tốc của người so với thuyền.
Áp dụng công thức cộng vận tốc ta có:

\(\overrightarrow{v_1}=\overrightarrow{v_0}+\overrightarrow{v_2}\leftrightarrow v_1=v_0-v_2\left(2\right)\)

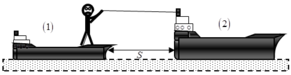
Kí hiệu \(1\) là chiều dài của thuyền và \(t\) là thời gian người đi từ mũi đến lái.
Ta có: \(v_0=\frac{1}{t};v_2=\frac{s}{t},s\) là đoạn đường thuyền đi được trong thời gian \(t\)

Từ đó :  \(v_1=v_0-v_2=\frac{1-s}{t}\)

Theo \(\left(1\right)\): \(mv_1=Mv_2\)

Suy ra:  \(m\frac{1-s}{t}=M\frac{s}{t}\leftrightarrow s=\frac{ml}{m+M}=1m\)

Khi người đi từ mũi đến lái thì động lượng của người bằng , với  là vận tốc của người đối với bờ sông, còn thuyề sẽ có động lượng , với  là vận tốc của thuyền đối với bờ.
áp dụng định luật bảo toàn động lượng ta suy ra: 
dấu trừ cho thấy thuyền chuyển động ngược chiều với người.
chọn chiều dương là chiều chuyển động của người và kí hiệu  là vận tốc người so với thuyền.
Áp dụng công thức cộng vận tốc và chiếu ta được:
ta có ,, s là đoạn đường thuyền dịch chuyển trong thời gian t.
từ đó:.mà .từ đó ta được 

mk gửi nhầm môn 

hihi

gửi nhầm môn có gì phải khóc

Chọn đáp án D

?  Lời giải:

+ Hợp lực tác dụng vào mỗi thuyền: 

Chọn đáp án B

?  Lời giải:

Đáp án D

Hợp lực tác dụng vào mỗi thuyền 

mọi người giúp e vs a