Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔMAO vuông tại A và ΔNBO vuông tại B có:
OA = OB (GT)
góc O chung
=> ΔMAO = ΔNBO (cạnh huyền - góc nhọn)
=> OM = ON ( 2 cạnh tương ứng ) → đpcm
Ta có OA + AN = ON
OB + BM = OM
mà OM = ON ( cm trên ); OA = OB
=> AN = BM → đpcm
b) Xét ΔNOH và ΔMOH có;
ON = OM (cm trên)
OH chung
NH = MH (suy từ gt)
=> ΔNOH = ΔMOH (c.c.c)
=> góc NOH = MOH ( 2 góc tương ứng )
Do đó OH là tia pg của góc xOy → đpcm (1)
c) Vì ΔMAO = ΔNBO nên góc OMA = ONB (2 góc tương ứng) hay ANI = BMI.
Xét ΔNAI và ΔMBI có:
góc ANI = BMI (cm trên)
AN = BM ( câu a)
góc NAI = MBI (= 90 )
=> ΔNAI = ΔMBI ( g.c.g )
=> AI = BI (2 cạnh tương ứng)
Xét ΔAOI và ΔBOI có :
AI = BI (cm trên)
góc OAI = OBI (=90)
OI chung
=> ΔAOI = ΔBOI ( c.g.c )
=> góc AOI = BOI ( 2 góc tương ứng )
Do đó OI là tia pg của xOy (2)
Từ (1) ở câu b và (2) suy ra O, H, I thẳng hàng.
Chúc học tốt nguyen thi minh nguyet 
a) Xét t/g OAM vuông tại A và t/g OBN vuông tại B có:
OA = OB (gt)
O là góc chung
Do đó, t/g OAM = t/g OBN ( cạnh góc vuông và góc nhọn kề)
=> AMO = BNO (2 góc tương ứng)
OM = ON (2 cạnh tương ứng) (1)
Lại có: OB = OA (gt)
=> OM - OB = ON - OA
=> BM = AN (2)
(1) và (2) là đpcm
b) Xét t/g HAN vuông tại A và t/g HBM vuông tại B có:
AN = BM (câu a)
ANH = BMH (câu a)
Do đó, t/g HAN = t/g HBM ( cạnh góc vuông và góc nhọn kề)
=> HN = HM (2 cạnh tương ứng)
Dễ dàng c/m t/g NOH = t/g MOH (c.c.c)
=> NOH = MOH (2 góc tương ứng)
=> OH là phân giác NOM hay OH là phân giác xOy (đpcm)
c) Dễ dàng c/m t/g NOI = t/g MOI (c.c.c)
=> NOI = MOI (2 góc tương ứng)
=> OI là phân giác NOM
Mà OH cũng là phân giác NOM
Nên O,H,I thẳng hàng (đpcm)
a: Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
b: Xét ΔOAC và ΔOBD có
\(\widehat{AOC}\) chung
OA=OB
\(\widehat{OAC}=\widehat{OBD}\)
Do đó; ΔOAC=ΔOBD
Suy ra: AC=BD
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOM}\) chung
Do đó: ΔOAM=ΔOBN
Suy ra OM=ON
b: Xét ΔBHM vuông tại B và ΔAHN vuông tại A có
BM=AN
\(\widehat{BHM}=\widehat{AHN}\)
Do đó: ΔBHM=ΔAHN
Suy ra: HN=HM
mà OM=ON
và IM=IN
nên O,H,I thẳng hàng
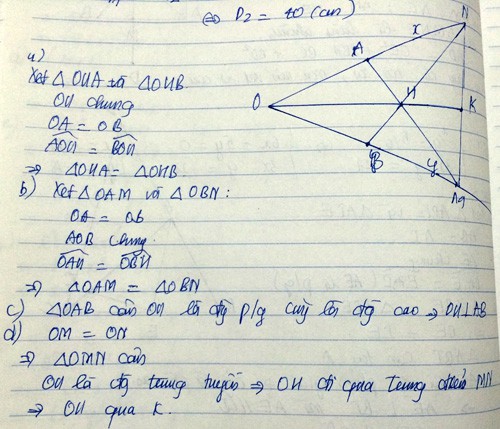
a) Sửa lại là \(\Delta AOM=\Delta BOM\) nhé.
Vì \(Ot\) là tia phân giác của \(\widehat{xOy}\left(gt\right)\)
Mà \(\)\(AB\) cắt \(Ot\) tại \(M\left(gt\right)\)
=> \(OM\) là tia phân giác của \(\widehat{xOy}.\)
Hay \(OM\) là tia phân giác của \(\widehat{AOB}.\)
Xét 2 \(\Delta\) \(AOM\) và \(BOM\) có:
\(AO=BO\left(gt\right)\)
\(\widehat{AOM}=\widehat{BOM}\) (vì \(OM\) là tia phân giác của \(\widehat{AOB}\))
Cạnh OM chung
=> \(\Delta AOM=\Delta BOM\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta AOM=\Delta BOM.\)
=> \(AM=BM\) (2 cạnh tương ứng).
c) Vì \(AM=BM\left(cmt\right)\)
=> M là trung điểm của \(AB.\)
Xét \(\Delta AOB\) có:
\(OA=OB\left(gt\right)\)
=> \(\Delta AOB\) cân tại \(O.\)
Có M là trung điểm của \(AB\left(cmt\right).\)
=> \(OM\) là đường trung tuyến của \(\Delta AOB.\)
=> \(OM\) đồng thời là đường cao của \(\Delta AOB.\)
=> \(OM\perp AB.\)
Mà \(AB\) // \(CD\left(gt\right)\)
=> \(OM\perp CD\)
Hay \(OH\perp CD\left(đpcm\right).\)
Chúc bạn học tốt!