a) Xét △ABD và △ACE có:

           AB = AC (gt)

           \(\widehat{A}\) chung

           AD = AE (gt)

\(\Rightarrow\)△ABD = △ACE (c.g.c)

\(\Rightarrow\)DB = EC (cặp cạnh tương ứng)

b) Ta có :△ABD = △ACE

\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)  (cặp góc tương ứng)

Mà \(\widehat{ABC}=\widehat{ACB}\) ( △ABC cân tại đỉnh A)

\(\Rightarrow\widehat{ABC}-\widehat{B_1}=\widehat{ACB}-\widehat{C_1}\)

\(\Rightarrow\widehat{OBC}=\widehat{OCB}\)

\(\Rightarrow\)△OBC cân tại đỉnh O

\(\Rightarrow\)OB = OC

Ta có: DB = EC (cmt)

           OB = OC

\(\Rightarrow\)DB - OB = EC - OC

\(\Rightarrow\)OE = OD

\(\Rightarrow\)△ODE cân đỉnh O (ĐPCM)

c) △OBC cân tại đỉnh O

\(\Rightarrow\)\(\widehat{OCB}=\frac{180^o-\widehat{BOC}}{2}\)

    △ODE cân tại đỉnh O

\(\Rightarrow\widehat{DEO}=\frac{180^o-\widehat{DOE}}{2}\)

Mà \(\widehat{BOC}=\widehat{DOE}\)(đối đỉnh)

\(\Rightarrow\widehat{DEO}=\widehat{OCB}\)

Vì 2 góc này nằm ở vị trí so le trong

\(\Rightarrow\)DE // BC (ĐPCM)

đúng đúng 

a) Xét ΔABD và ΔACE có:

AB=ACAB=AC (do ΔABC cân đỉnh A)

ˆA^ : góc chung

AD=AE (giả thiết)

⇒ΔABD=ΔACE (c.g.c)

⇒DB=EC (hai cạnh tương ứng)

b) ΔABD=ΔACE⇒ˆB1=ˆC1 (hai góc tương ứng)

Mà ˆABC=ˆACB (do ΔABC cân đỉnh A)

⇒ˆABC−ˆB1=ˆACB−ˆC1

⇒ˆOBC=ˆOCB

⇒ΔOBC cân đỉnh O (đpcm)

Sửa câu c:  DE // BE thành DE // BC nhé

Bài giải:

a, Vì △ABC cân tại A (gt) => AB = AC

Xét △BAD và △CAE 

Có: AB = AC (cmt)

  BAC là góc chung

      AD = AE (gt)    

=> △BAD = △CAE (c.g.c)

=> DB = CE (2 cạnh tương ứng)

b, Vì △BAD = △CAE (cmt)

=> ABD = ACE (2 góc tương ứng) và ADB = CEA (2 góc tương ứng)

Ta có: CEA + CEB = 180^o (2 góc kề bù)

ADB + BDC = 180^o (2 góc kề bù)

Mà ADB = CEA (cmt)

=> CEB = BDC 

Lại có: AB = AE + EB

AC = AD + DC

Mà AB = AC (gt) ; AD = AE (gt)

=> EB = DC

Xét △BOE và △COD

Có: OBE = OCD (cmt)

         BE = CD (cmt)

      BEO = CDO (cmt)

=> △BOE = △COD (g.c.g)

=> OB = OC (2 cạnh tương ứng) và OE = OD (2 cạnh tương ứng)

Xét △OED có: OE = OD (cmt) => △OED cân tại O

Xét △OBC có: OB = OC (cmt) => △OBC cân tại O

c, Xét △AOD có: AE = AD (gt) => △AOD cân tại A => AED = (180^o - EAD) : 2    (1)

Vì △ABC cân tại A (gt) => ABC = (180^o - BAC) : 2                                               (2)

Từ (1) và (2) => AED = ABC

Mà 2 góc này nằm ở vị trí đồng vị

=> ED // BC (dhnb)

ok thanks

`a)` 

Có `Delta ABC ` cân tại `A(GT)=>AB=AC`

Xét `Delta ADB` và `Delta AEC` có:

`{:(AB=AC(cmt)),(hat(A)-chung),(AD=AE(GT)):}}`

`=>Delta ADB=Delta AEC(c.g.c)(đpcm)`

`b)`

Có `Delta ABC` cân tại `A=>hat(ABC)=hat(ACB)`

`=>hat(EBC)=hat(DCB)`

mà `hat(B_1)=hat(C_1)(Delta ADB=Delta AEC)`

`hat(B_1)+hat(B_2)=hat(EBC)`

`hat(C_1)+hat(C_2)=hat(DCB)`

nên `hat(B_2)=hat(C_2)`

`=>Delta IBC` cân tại `I` 

`c)`

Có `AE=AD(GT)=>Delta AED` cân tại `A`

`=>hat(E_1)=(180^0-hat(A))/2(1)`

`Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2(2)`

Từ `(1)` và `(2)=>hat(E_1)=hat(ABC)`

mà `2` góc này ở vị trí đ/vị 

nên `ED////BC(đpcm)`

c.ơn nha

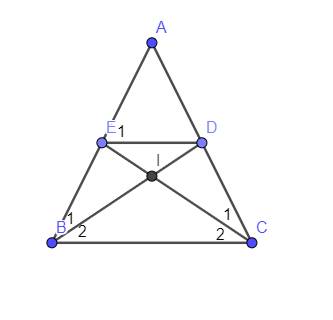
a, Xét tam giác ADB và tam giác AEC có :

AE = AD ( gt )

\(\widehat{A}\) chung

AB = AC ( gt )

=> \(\Delta ADB=\Delta AEC\left(c-g-c\right)\)

b, Do \(\Delta ADB=\Delta AEC\) ( câu a, )

=> \(\widehat{ABD}=\widehat{ACE}\) ( 2 góc tương ứng )

BD nằm giữa 2 tia EB và EC 

=> \(\widehat{EBD}+\widehat{CBD}=\widehat{B}\)

\(\Rightarrow\widehat{CBD}=\widehat{B}-\widehat{EBD}\) ( 1 )

CE nằm giữa 2 tia CD và CB 

\(\Rightarrow\widehat{BCE}+\widehat{DCE}=\widehat{C}\)

\(\Rightarrow\widehat{BCE}=\widehat{C}-\widehat{DCE}\) ( 2 )

Từ ( 1 ) và ( 2 ) 

=> \(\widehat{CBD}=\widehat{BCE}\) hay \(\widehat{IBC}=\widehat{ICB}\)

Xét tam giác IBC có 

\(\widehat{IBC}=\widehat{ICB}\)

=> tam giác IBC cân tại I

c, Xét tam giác AED có :

AE = AD ( gt )

=> Tam giác AED cân tại A

=> \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)( 3 )

Tam giác ABC cân tại A 

=> \(\widehat{B}=\dfrac{180^0-\widehat{A}}{2}\) ( 4 )

Từ ( 3 ) , ( 4) => \(\widehat{AED}=\widehat{B}\)

Đường thẳng AB bị 2 đường thẳng ED và BC cắt tạo thành cặp góc đồng vị bằng nhau \(\widehat{AED}=\widehat{B}\)

=> ED // BC ( đpcm)

điểm D thuộc cạnh AB*
-ghi lộn :"))

Bài 3: 

a: Xét ΔAIB và ΔCID có

IA=IC

góc AIB=góc CID

IB=ID

Do đó: ΔAIB=ΔCID

b: Xét tứ giác ABCD có

I là trung điểm chung của AC và BD

nên ABCD là hình bình hành

Suy ra: AD//BC va AD=BC

Bài 6: 

a: Xét ΔADB và ΔAEC có

AD=AE
góc A chung

AB=AC

Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có

EB=DC

BC chung

EC=BD

Do đó: ΔEBC=ΔDCB

Suy ra: góc OBC=góc OCB

=>ΔOBC cân tại O

=>OB=OC

=>OE=OD

=>ΔOED cân tại O

c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a: Xét ΔABD và ΔAED có

AB=AE

góc BAD=góc EAD

AD chung

=>ΔABD=ΔAED

b: ΔABD=ΔAED

=>góc AED=góc ABD=90 độ

c: Xét ΔAEF vuông tại A và ΔABC vuông tại B có

AE=AB

góc EAF chung

=>ΔAEF=ΔABC

=>AF=AC

d: DB=DE

mà DE<DC

nên DB<DC