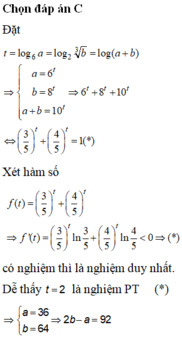Ta có: \(\sqrt{2}>0\)

\(\Rightarrow b\sqrt{2}\ge0\)

Mà \(a+b\sqrt{2}=0\)

\(\Rightarrow b=0,a=0\)

OH-YEAH^^                                                         , bn ơi b thuộc Q thì làm sao mà \(b\sqrt{2}\ge0\) được

Lời giải:
$|a+b|=|a-b|$

$\Rightarrow |a+b|^2=|a-b|^2$

$\Leftrightarrow (a+b)^2=(a-b)^2$

$\Leftrightarrow a^2+2ab+b^2=a^2-2ab+b^2$

$\Leftrightarrow 4ab=0$

$\Rightarrow a=0$ hoặc $b=0$ (đpcm)

b: (3x-2)^5+(5-x)^5+(-2x-3)^5=0

Đặt a=3x-2; b=-2x-3

Pt sẽ trở thành:

a^5+b^5-(a+b)^5=0

=>a^5+b^5-(a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5)=0

=>-5a^4b-10a^3b^2-10a^2b^3-5ab^4=0

=>-5a^4b-5ab^4-10a^3b^2-10a^2b^3=0

=>-5ab(a^3+b^3)-10a^2b^2(a+b)=0

=>-5ab(a+b)(a^2-ab+b^2)-10a^2b^2(a+b)=0

=>-5ab(a+b)(a^2-ab+b^2+2ab)=0

=>-5ab(a+b)(a^2+b^2+ab)=0

=>ab(a+b)=0

=>(3x-2)(-2x-3)(5-x)=0

=>\(x\in\left\{\dfrac{2}{3};-\dfrac{3}{2};5\right\}\)

bn oi, con cau a nx ma

Ta có:

Dấu “=” xảy ra khi và chỉ khi

Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.

Chọn B.

\(\left|a+b\right|=\left|a-b\right|\)

\(\Rightarrow\orbr{\begin{cases}a+b=a-b\\a+b=-\left(a-b\right)\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}a-a=-b-b\\a+b=-a+b\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}0=-2b\\a+a=b-b\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}b=0\\2a=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}b=0\\a=0\end{cases}}\)

1) Áp dụng bất đẳng thức AM - GM và bất đẳng thức Schwarz:

\(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\ge\dfrac{1}{a}+\dfrac{1}{\dfrac{a+b}{2}}\ge\dfrac{4}{a+\dfrac{a+b}{2}}=\dfrac{8}{3a+b}\ge8\).

Đẳng thức xảy ra khi a = b = \(\dfrac{1}{4}\).

2.

\(4=a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\Rightarrow a+b\le2\sqrt{2}\)

Đồng thời \(\left(a+b\right)^2\ge a^2+b^2\Rightarrow a+b\ge2\)

\(M\le\dfrac{\left(a+b\right)^2}{4\left(a+b+2\right)}=\dfrac{x^2}{4\left(x+2\right)}\) (với \(x=a+b\Rightarrow2\le x\le2\sqrt{2}\) )

\(M\le\dfrac{x^2}{4\left(x+2\right)}-\sqrt{2}+1+\sqrt{2}-1\)

\(M\le\dfrac{\left(2\sqrt{2}-x\right)\left(x+4-2\sqrt{2}\right)}{4\left(x+2\right)}+\sqrt{2}-1\le\sqrt{2}-1\)

Dấu "=" xảy ra khi \(x=2\sqrt{2}\) hay \(a=b=\sqrt{2}\)

3. Chia 2 vế giả thiết cho \(x^2y^2\)

\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\ge\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\)

\(\Rightarrow0\le\dfrac{1}{x}+\dfrac{1}{y}\le4\)

\(A=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\right)=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le16\)

Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)