Tìm x thuộc Z, biết : x2+3x+7 chia hết cho x+3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{6x+14}{2x-3}=\dfrac{3\left(2x-3\right)+23}{2x-3}=3+\dfrac{23}{2x-3}\Rightarrow2x-3\inƯ\left(23\right)=\left\{\pm1;\pm23\right\}\)
| 2x-3 | 1 | -1 | 23 | -23 |
| x | 2 | 1 | 13 | -10 |
tương tự

Bài 1
a)x-13+(-20)=-3
x-13=(-3)-(-20)
x-13=17
x=17+13
x=30
b)Ix-3I=3
=>x-3=3
x-3=-3
=>x=6
x=0
vậy x thuộc {0;6}
bài 2
Ta có: (3x+7) chia hết cho (x+2)
=> 3.x-9+7+9chia hết cho x+2
=>(3.x-9)+16 chia hết cho x+2
mà 3x-9 chia hết cho x+2
=>16 chia hết cho x+2
=>x+2 thuộc Ư(16)
=>x+2 thuộc {1;2;4;8;16}
x thuộc {-1;0;2;6;14}

1.
\(3x+4⋮x-3\)
\(\Rightarrow3x-9+9+4⋮x-3\)
\(\Rightarrow3x-3\cdot3+13⋮x-3\)
\(\Rightarrow3\left(x-3\right)+13⋮x-3\)
\(3\left(x-3\right)⋮x-3\)
\(\Rightarrow13⋮x-3\)
\(\Rightarrow x-3\inƯ\left(13\right)\) ; \(x\in Z\Rightarrow x-3\in Z\)
\(\Rightarrow x-3\in\left\{-1;1;13;-13\right\}\)
\(\Rightarrow x\in\left\{2;4;16;-10\right\}\)
vậy_____
2.
\(x^2+7⋮x+1 \)
\(\Rightarrow x\cdot x+7⋮x+1\)
\(\Rightarrow x\cdot x+x-x+7⋮x+1\)
\(\Rightarrow x\cdot\left(x+1\right)-x+7⋮x+1\)
\(x\cdot\left(x+1\right)⋮x+1\)
\(\Rightarrow x+7⋮x+1\)
\(\Rightarrow x+1+6⋮x+1\)
\(x+1⋮x+1\)
\(\Rightarrow6⋮x+1\)
\(\Rightarrow x+1\inƯ\left(6\right)\) ; \(x\in Z\Rightarrow x+1\in Z\)
\(\Rightarrow x+1\in\left\{-1;1;-2;2;-3;3;-6;6\right\}\)
\(\Rightarrow x\in\left\{-2;0;-3;1;-4;2;-7;5\right\}\)
vậy______
3x+4 chia hết cho x-3
3x-9+13 chia hết cho x-3
3.(x-3)+13 chia hết cho x-3
ma 3.(x-3) chia hết cho x-3
13 chia hết cho x-3
x-3 thuoc U(13)={1,-1,13,-13}
suy ra x thuộc{2,4,16,-10}
2x-1 chia hết cho x+1
2x+2-3 chia hết cho x+1
2(x+1)-3 chia hết cho x+1
3 chia hết cho x+1
x+1 thuộc Ư(3)={1,-1,3,-3}
suy ra x thuộc {0,2,-2,-4}
CHÚC BẠN HỌC TỐT NHÉ !!!!!!
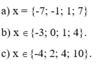
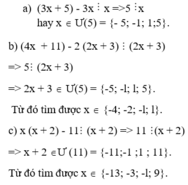
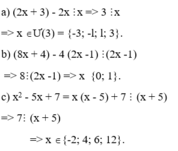

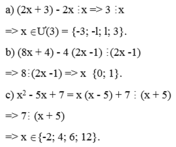
Để \(x^2+3x+7\) chia hết cho x+3 thì:
\(\frac{x^2+3x+7}{x+3}\in Z\). Đặt A\(=\frac{x^2+3x+7}{x+3}\)
Ta có: \(\frac{x^2+3x+7}{x+3}=\frac{x^2+6x+9-3x-9+7}{x+3}\)
\(=\frac{\left(x^2+6x+9\right)-\left(3x+9\right)+7}{x+3}\)
\(=\frac{\left(x^2+3x+3x+9\right)-3\left(x+3\right)+7}{x+3}\)\(=\frac{\left[x\left(x+3\right)+3\left(x+3\right)\right]-3\left(x+3\right)+7}{x+3}\)
\(=\frac{\left(x+3\right)\left(x +3\right)-3\left(x+3\right)+7}{x+3}\)\(=\frac{\left(x+3\right)^2}{x+3}-\frac{3\left(x+3\right)}{x+3}+\frac{7}{x+3}\)\(=x+3-3+\frac{7}{x+3}\)
\(=x+\frac{7}{x+3}\)
Do đó, để A thuộc Z thì \(7⋮x+3\)
Khi đó: \(x+3\inƯ\left(7\right)\)\(\Rightarrow x+3\in\left\{1;-1;7;-7\right\}\)\(\Rightarrow x\in\left\{-2;-4;4;-10\right\}\)
Cảm ơn Nguyễn Phương Thảo nhiều lắm, bạn làm đúng rồi! Tớ đã dùng cả 2 nick để k đúng cho bạn đó!