Cho hình bình hành ABCD. Phân giác của A và D cắt các đường chéo BD và AC lần lượt tại M và N. Chứng minh MN // AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 11 2023
Gọi O là giao điểm AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔDAC có DN là phân giác
nên \(\dfrac{AN}{NC}=\dfrac{AD}{DC}\)
Xét ΔBAD có AM là phân giác
nên \(\dfrac{DM}{MB}=\dfrac{AD}{AB}\)
=>\(\dfrac{DM}{MB}=\dfrac{AD}{DC}\)
=>\(\dfrac{AN}{NC}=\dfrac{DM}{MB}\)
=>\(\dfrac{CN}{AN}=\dfrac{MB}{DM}\)
=>\(\dfrac{CN}{AN}+1=\dfrac{MB}{MD}+1\)
=>\(\dfrac{CN+AN}{AN}=\dfrac{MB+MD}{MD}\)
=>\(\dfrac{AC}{AN}=\dfrac{BD}{MD}\)
=>\(\dfrac{AN}{MD}=\dfrac{AC}{BD}=\dfrac{2\cdot OA}{2\cdot OD}=\dfrac{OA}{OD}\)
=>\(\dfrac{AN}{OA}=\dfrac{MD}{OD}\)
Xét ΔOAD có \(\dfrac{AN}{AO}=\dfrac{DM}{DO}\)
nên MN//AD
25 tháng 12 2021
Ta có AM,DN lần lượt là phân giác \(\Delta ABD,\Delta ADC\)
\(\Rightarrow\dfrac{MD}{MB}=\dfrac{AD}{AB};\dfrac{NA}{NC}=\dfrac{AD}{DC}\)
Mà \(AB=CD\left(gt\right)\\ \Rightarrow\dfrac{MD}{MB}=\dfrac{NA}{NC}\Rightarrow\dfrac{MD+AB}{MB}=\dfrac{NA+NC}{NC}\\ \Rightarrow\dfrac{BD}{MB}=\dfrac{CA}{NC}\)
Theo đlí Talet đảo ta được MN//BC
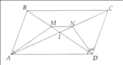
Gọi \(I\) là giao điểm điểm \(BD\)và \(AC\).
Xét \(\Delta ABD\)có tia p.giác \(AM\)có: \(\frac{AB}{AD}=\frac{BM}{DM}\)
Tương tự ta có: \(\frac{CD}{AD}=\frac{CN}{AN}\)
Mà: \(AB=CD\Rightarrow\frac{BM}{DM}=\frac{CN}{AN}\)
Từ trên ta suy ra: \(\frac{BM}{DM}+1=\frac{CN}{AN}+1\Leftrightarrow\frac{BD}{DM}=\frac{AC}{AN}\Leftrightarrow\frac{AI}{DM}=\frac{AI}{AN}\)
\(\Rightarrow MN//AD\left(đpcm\right)\)