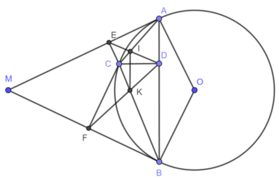
cho MA,MB là 2 tiếp tuyến của (O). C là điểm thuộc cung nhỏ AB. Vẽ \(CD\perp AB\) ,\(CE\perp MA,CF\perp MB\) .
a, CM tứ giác DAEC nội tiếp
b,CM \(CE.CF=CD^2\)
c AC cắt ED tại H,BC cắt DF tại K. CM tứ giác CHDK nội tiếp
d, CM \(HK//AB\)
e, CM , HK là tiếp tuyến của 2 đtròn ngoại tiếp 2 tam giác CKF,CHE
g,gọi I là giao điểm thứ 2 của 2 đtròn ở câu e, CM \(CI\) đi qua trung điểm của AB
làm giúp mk câu e vs g nha mấu câu trc mk làm đc rùi
\(thankyou\)




Câu a, Tứ giác AECD có : CEA^=90* ; CDA^=90*
=>CEA^+CDA^=180*
=>AECD nội tiếp
Câu b, Xét tam giác BCD và tam giác ACE , có :
BDC^=CEA^=90*
CBA^=CAE^ ( góc nội tiếp ; góc ở tâm cùng chắn một cung )
=>Tam giác BCD ~ Tam giác ACE
=> BC/AC=CD/CE=BD/AE (1)
Xét tam giác CFB và tam giác CDA , có :
CFB^=CDA^=90*
CBF^=CAD^ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung )
=>Tam giác CFB ~ tam giác CDA ( g - g )
=>CF/CD=CB/CA=BF/AD (2)
Từ (1) và (2)
=>CD/CE=CF/CD
=>CD^2=CE.CF
Chúc bạn học tốt !