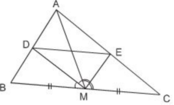
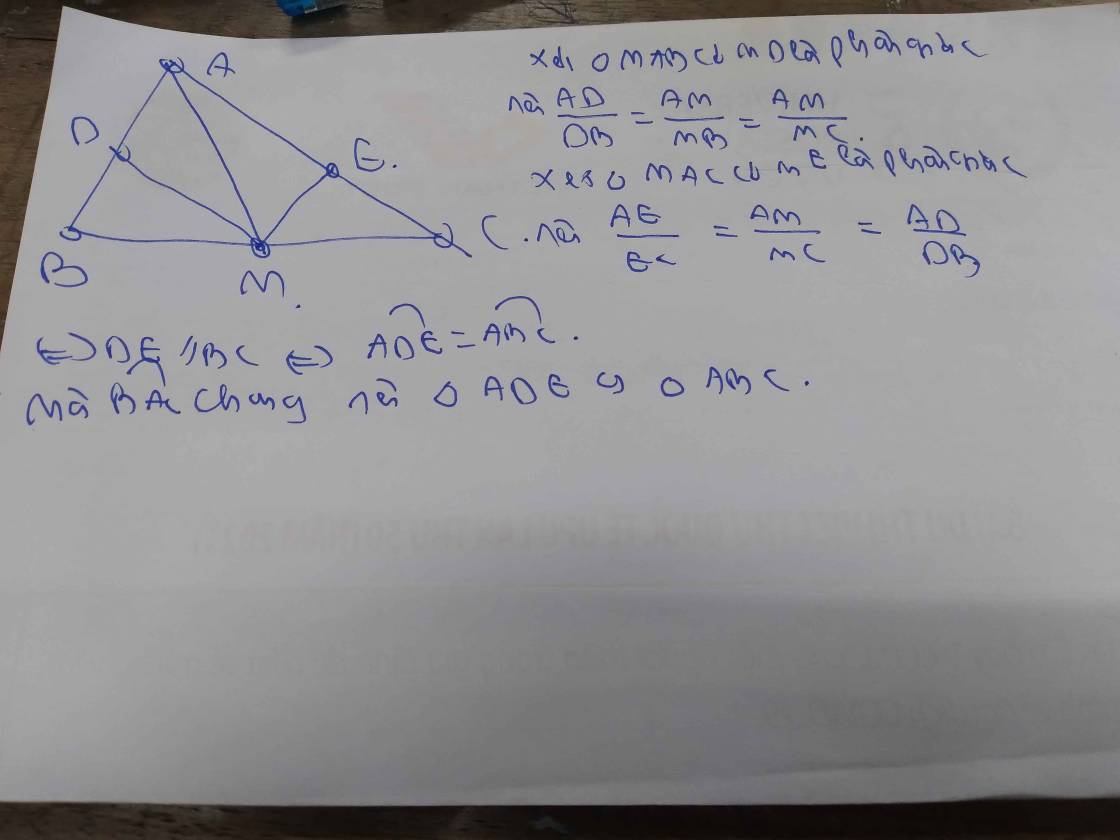
Cho tam giác ABC với đường trung tuyến BI. Tia phân giác Tia phân giác của góc AIB cắt cạnh AB ở M. Tia phân giác của góc BIC cắt cạnhBC ở N. Chứng minh rằng MN//AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lý phân giác cho tam giác ABM:
\(\dfrac{AM}{BM}=\dfrac{AD}{BD}\) (1)
Áp dụng định lý phân giác cho tam giác ACM:
\(\dfrac{AM}{CM}=\dfrac{AE}{CE}\) (2)
Mà AM là trung tuyến \(\Rightarrow BM=CM\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{CE}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+CE}\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\Rightarrow DE||BC\) (định lý talet đảo)

Xét tam giác ABM có:
MD là tia phân giác của góc AMB
=>\(\dfrac{DA}{DB}=\dfrac{AM}{BM}\)(Tính chất đường phân giác)(1)
CMTT:\(\dfrac{EA}{EC}=\dfrac{AM}{MC}\)(2)
Ta có: BM=MC(AM là trung tuyến nên M là trung điểm BC)
=>\(\dfrac{AM}{BM}=\dfrac{AM}{MC}\)(3)
Từ (1),(2) và (3)
=>\(\dfrac{DA}{DB}=\dfrac{EA}{EC}\)
=>DE//BC(định lí ta let áp dụng trong tam giác ABC)
Vì ME là tia p/g của \(\widehat{AMC}\) nên \(\dfrac{AE}{AM}=\dfrac{CE}{CM}\Leftrightarrow\dfrac{AE}{CE}=\dfrac{AM}{CM}\)(1)
Vì MD là tia p/g của \(\widehat{AMB}\) nên \(\dfrac{AD}{AM}=\dfrac{BD}{BM}\Leftrightarrow\dfrac{AD}{BD}=\dfrac{AM}{BM}\)(2)
\(\dfrac{AM}{CM}=\dfrac{AM}{BM}\)(3)
TỪ (1)(2)(3)=>\(\dfrac{AE}{CE}=\dfrac{AD}{BD}\)
\(\Rightarrow DE//BC\)
BC ko phải DC đk

Xét ΔBNC có
NF là phân giác
nên BF/FC=BN/NC=BN/NA(1)
Xét ΔBNA có NE là phân giác
nên BE/EA=BN/NA(2)
Từ (1) và (2) suy ra BF/FC=BE/EA
hay FE//AC