Mn ơi , giúp mình giải bài này .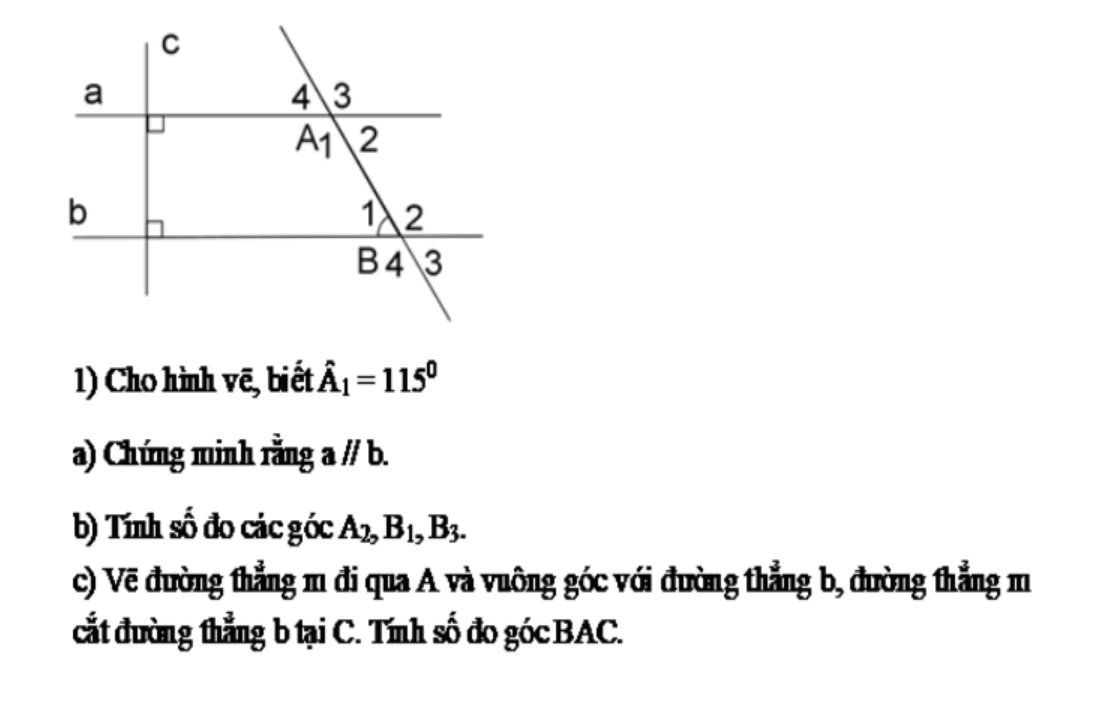
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 8:
a: Thay x=16 vào P, ta được:
\(P=\dfrac{4+2}{4-1}=\dfrac{6}{3}=2\)
b: Thay \(x=3+2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{\sqrt{2}+1+2}{\sqrt{2}+1-1}=\dfrac{3+\sqrt{2}}{\sqrt{2}}=3\sqrt{2}+2\)

Bài 20
Hệ (1) ⇔ \(\left\{{}\begin{matrix}1< x< 4\\x\le m-1\end{matrix}\right.\)
Đặt hai tập hợp A = (1 ; 4) và B = (\(-\infty\); m - 1]
Nếu m - 1 ≤ 1 tức m ≤ 2 thì A \(\cap\) B = ∅, hệ vô nghiệm
Nếu 1 < m - 1 < 4 tức 2 < m < 5 thì
A \(\cap\) B = (1; m - 1), tập nghiệm của hệ là (1; m - 1)
Nếu m - 1 ≥ 4 tức m ≥ 5 thì A \(\subset\) B. Tập nghiệm của hệ là A = (1; 4)

ý bạn là \(x-y-z=-33?\)
Ta có \(2x=3y=5z\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x-y-z}{15-10-6}=\dfrac{-33}{-1}=33\\ \Rightarrow\left\{{}\begin{matrix}x=33\cdot15=495\\y=33\cdot10=330\\z=33\cdot6=198\end{matrix}\right.\)

giúp mk giải gấp 2 bài này với chiều tầm 3h mình qua lấy nha.cảm ơn mọi người nhiều ah.

a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
) Xét ΔOBH và ΔODA có
OB=OD(gt)
ˆBOH=ˆDOABOH^=DOA^(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: ˆOHB=ˆOADOHB^=OAD^(hai góc tương ứng)
mà ˆOHB=900OHB^=900(gt)
nên ˆOAD=900OAD^=900
hay AH⊥⊥AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
ˆAOE=ˆHOCAOE^=HOC^(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE

\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)

Em tách nhỏ ra rồi hỏi nhe!! VD như 1 bài hỏi 1 lần á
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)

1) Ta có: \(\dfrac{1}{\sqrt{3}-1}+\dfrac{1}{4+2\sqrt{3}}-\dfrac{2}{\sqrt{3}}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1}{2}+\dfrac{2-\sqrt{3}}{2}-\dfrac{2\sqrt{3}}{3}-\dfrac{3}{2}\)
\(=\dfrac{\sqrt{3}+1+2-\sqrt{3}-3}{2}-\dfrac{2\sqrt{3}}{3}\)
\(=-\dfrac{2\sqrt{3}}{3}\)
3) Ta có: \(\dfrac{\sqrt{10}+\sqrt{15}}{\sqrt{8}+\sqrt{12}}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)}{2\left(\sqrt{2}+\sqrt{3}\right)}-\dfrac{3\sqrt{5}}{4}\)
\(=\dfrac{2\sqrt{5}-3\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{4}\)


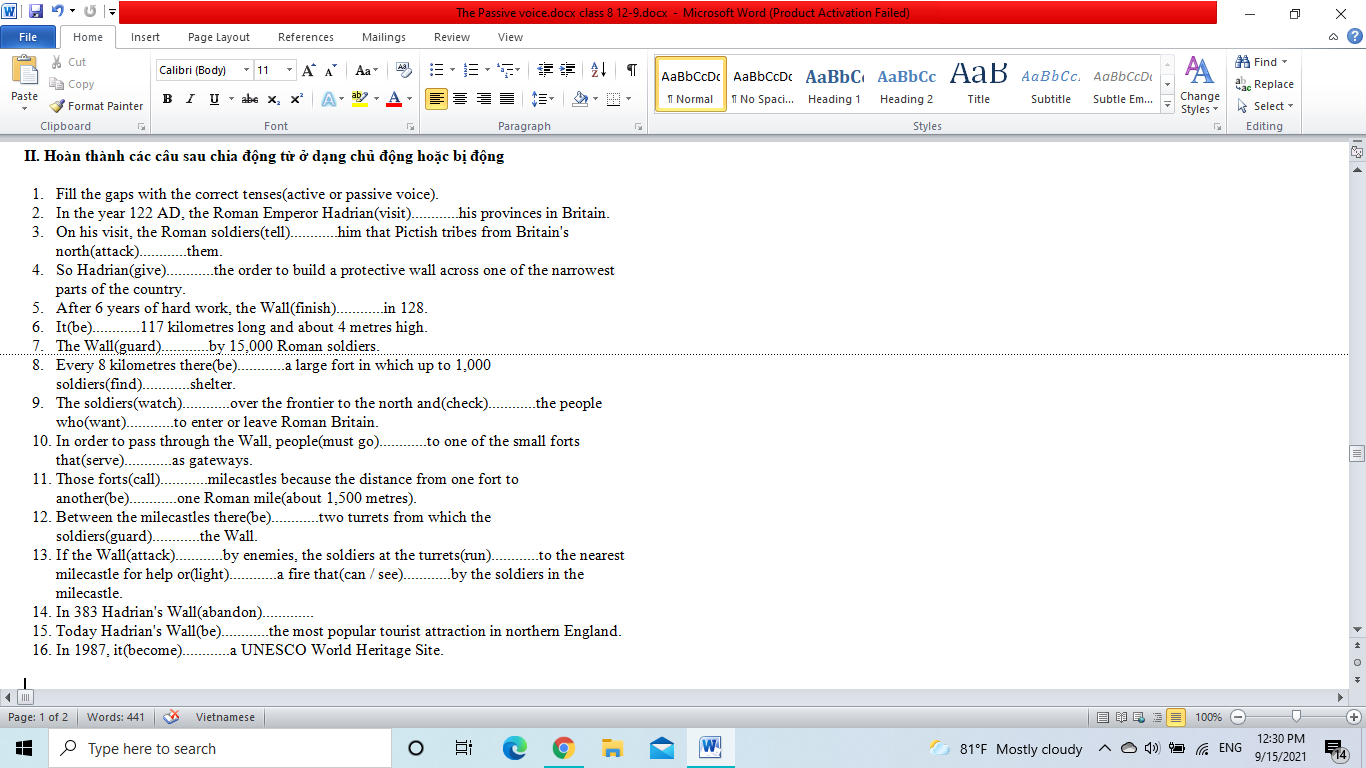
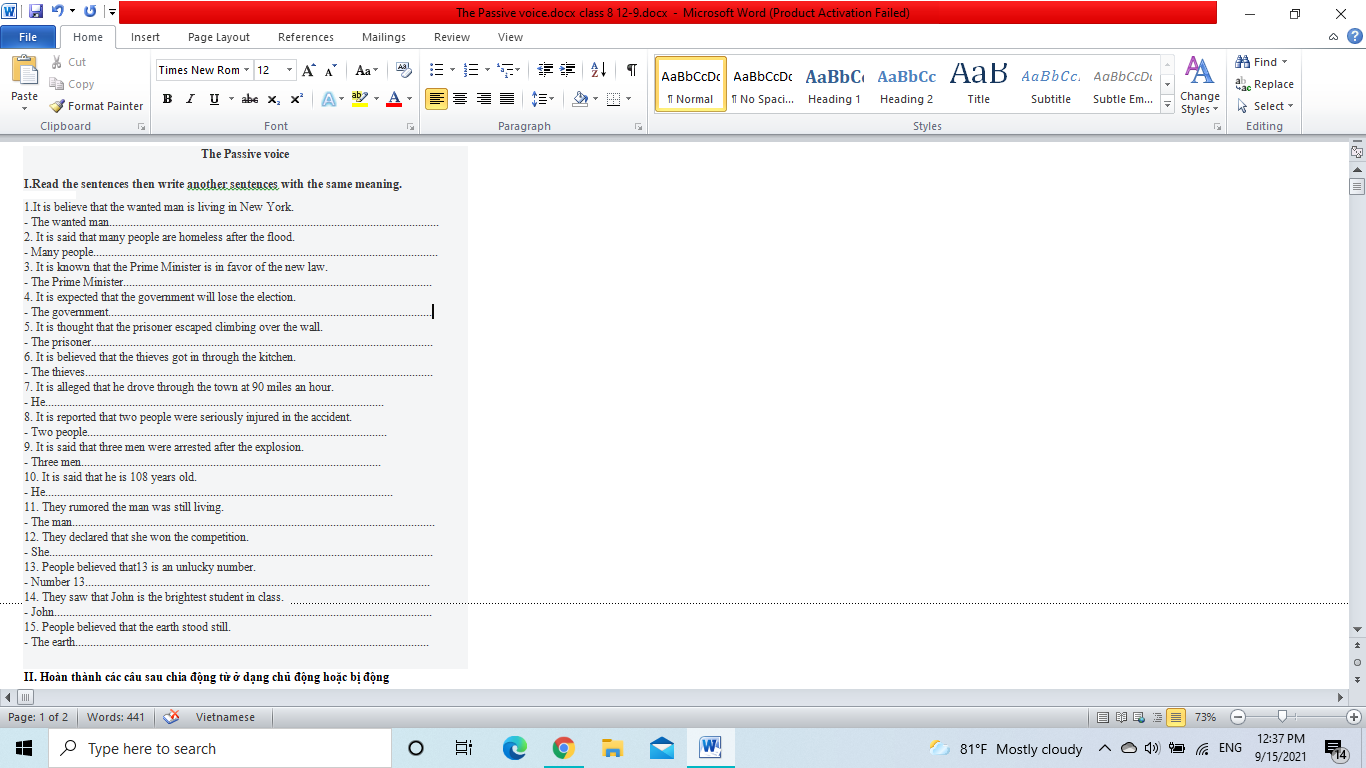 mn ơi giải giúp mk 2 bài này với chiều tầm 3h mình quay lại lấy bài nhé cảm ơn mn rất nhiều.
mn ơi giải giúp mk 2 bài này với chiều tầm 3h mình quay lại lấy bài nhé cảm ơn mn rất nhiều.




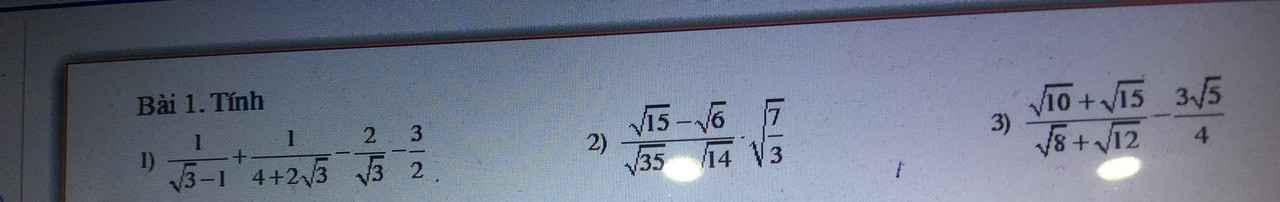
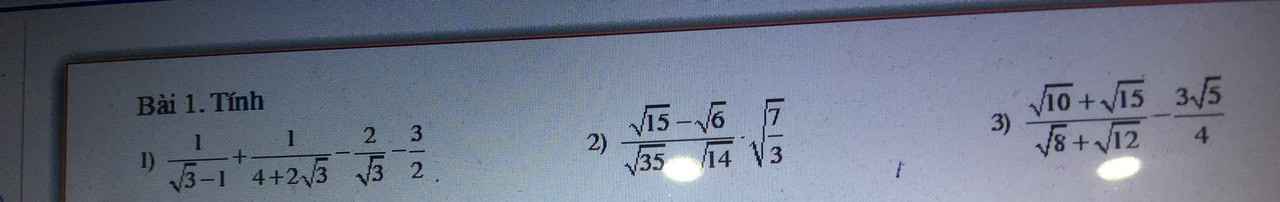
a) Ta có: a⊥c,b⊥c
=> a//b
b) \(\widehat{A_2}+\widehat{A_1}=180^0\)(kề bù)
\(\Rightarrow\widehat{A_2}=180^0-115^0=65^0\)
\(\widehat{B_1}=\widehat{A_2}=65^0\)(so le trong do a//b)
\(\Rightarrow\widehat{B_1}=\widehat{B_3}=65^0\)(đối đỉnh)
Còn câu C bạn