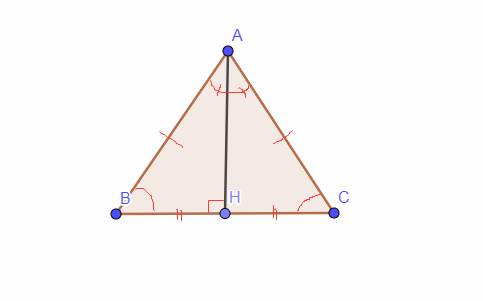
cho tam giác abc cân có AB=AC=5cm BC =8cm kẻ AH vuông góc với BC tại H cm H là trung điểm của BC và AH là tia phân giác của góc BAC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từng bài 1 thôi nha!
Mình làm bài 3 cho dễ
Bn tự vẽ hình
a) CM tg ABH=tg ACH (ch-cgv)
=> HC=HB=2 góc tương ứng
Nên H là trung điểm BC
=> HB=HC=BC:2=8:2=4 ; góc BAH= góc CAH
b) Có: tg ABH vuông tại H (AH vuông góc BC)
=> AH2+BH2=AB2 => AH2+42=52 => AH2=9
Mà AH>O Nên AH=3
c) Xét tg ADH và tg AEH có:
\(\Delta ADH=\Delta AEH\left(ch-gh\right)\hept{\begin{cases}\widehat{ADH}=\widehat{AEH}=90^o\\AHcanhchung\\\widehat{DAH}=\widehat{EAH}\left(\Delta ABH=\Delta ACH\right)\end{cases}}\)
=> HD=HE(2 góc tương ứng)
=> tg HDE cân tại H

a: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là phân giác của góc BAC
c: ΔABC cân tại A
mà AH là trung tuyến
nên AH là trung trực của BC
=>I nằm trên trung trực của BC
=>IB=IC
d: Xet ΔABN có góc ABN=góc ANB=góc MBC
nên ΔABN can tại A
=>AB=AN
e: Xét ΔABC co
BM,AM là phân giác
nên M là tâm đừog tròn nội tiếp
=>CM là phân giác của góc ACB
Xét ΔHCM vuông tại H và ΔKCM vuông tại K có
CM chung
góc HCM=góc KCM
=>ΔHCM=ΔKCM
=>MH=MK

a) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC).
=> AH là đường phân giác góc A (Tính chất tam giác cân).
b) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC).
=> AH là đường trung tuyến (Tính chất tam giác cân).
=> H là trung điểm của BC.
=> BH = HC = \(\dfrac{1}{2}\) BC = \(\dfrac{1}{2}\).8 = 4 (cm).
Xét tam giác AHB vuông tại A:
Ta có: \(AB^2=AH^2+BH^2H^2\) (Định lý Pytago).
=> \(5^2=AH^2+4^2.\) => \(AH^2=5^2-4^2=9.\)
=> AH = 3 (cm).
c) Xét tam giác AHD vuông tại D và tam giác AHE vuông tại A:
AH chung.
Góc DAH = Góc EAH (AH là đường phân giác góc A).
=> Tam giác AHD = Tam giác AHE (ch - gn).
=> HD = HE (2 cạnh tương ứng).
=> Tam giác DHE cân tại H.

a, Xet tam giac ABH va tam giac ACH co
AH chung ,goc B= goc C ;AB=AC
=>tam giac ABH = tam giac ACH
=>HB=HC (2 canh tuong ung )
=>H la trung diem cua BC
(Bạn tự vẽ hình giùm)
a/ \(\Delta AHB\)vuông và \(\Delta AHC\)vuông có: AB = AC (\(\Delta ABC\)cân tại A)
Cạnh AH chung
=> \(\Delta AHB\)vuông = \(\Delta AHC\)vuông (cạnh huyền - cạnh góc vuông) => HB = HC => H là trung điểm BC (đpcm)
b/ Ta có \(\Delta AHB\)= \(\Delta AHC\)(cm câu a) => \(\widehat{BAH}=\widehat{HAC}\)(hai góc tương ứng) => AH là tia phân giác của \(\widehat{BAC}\)(đpcm)
c/ Nối I với H, K với H.
\(\Delta IHB\)vuông và \(\Delta KHC\)vuông có: HB = HC (cm câu a)
\(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
=> \(\Delta IHB\)vuông = \(\Delta KHC\)vuông (cạnh huyền - góc nhọn) => IB = KC (hai cạnh tương ứng) (1)
và AB = AC (\(\Delta ABC\)cân tại A) (2)
Lấy (2) trừ (1) => AB - IB = AC - KC
=> AI = AK => \(\Delta AIK\)cân tại A => \(\widehat{AIK}=\frac{180^o-\widehat{A}}{2}\)
và \(\widehat{B}=\frac{180^o-\widehat{A}}{2}\)(\(\Delta ABC\)cân tại A)
=> \(\widehat{AIK}=\widehat{B}\)ở vị trí đồng vị => IK // BC (đpcm)

`\color{blue}\text {#DuyNam}`
`a,` Vì Tam giác `ABC` cân `-> AB=AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABH` và Tam giác `ACH` có:
\(\widehat{B}=\widehat{C}\)
`AB = AC`
`=>` Tam giác `ABH =` Tam giác `ACH (ch-gn)`
`-> HB=HC (2` cạnh tương ứng `)`
`-> H` là trung điểm của `BC`
`b,` Vì Tam giác `ABH =` Tam giác `ACH (a)`
`->`\(\widehat{BAH}=\widehat{CAH}\) `(2` góc tương ứng `)`
`-> AH` là tia phân giác của \(\widehat{BAC}\)

a/ xét tam giác ABC cân tại A ta có
AH là đường phân giác(gt)
=> AH là đường trung tuyến; AH là đường cao
=>H là trung điểm của BC và AH vuông góc với BC
\(\)
b/ ta có: H là trung điểm của BC
\(\Rightarrow BH=\frac{1}{2}BC\)
\(\Rightarrow BH=6cm\)
xét tam giác ABH vuông tại H ta có
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH^2=AB^2-BH^2\)
\(\Rightarrow AH^2=64\)
\(\Rightarrow AH=8cm\)
ta có
\(S_{ABC}=\frac{AH.BC}{2}\)
\(S_{ABC}=48cm^2\)
c/ xét tam giác MBH vuông tại M và tam giác NCH vuông tại N ta có
BH=HC(H là trung điểm của BC)
góc MBH=góc NCH (tam giác ABC vuông tại A)
=> tam giác MBH=tam giác NCH (ch-gn)
=> MH=NH (2 cạnh tuong ứng)
cmtt tam giác BGH=tam giác CNH (ch-gn)
=> QH=NH(2 cạnh tương ứng)
mà MH=NH(cmt)
nên QH=MH
=> tam giác GHM cân tại H
\(\)

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

Hình tự vẽ
Xét \(\Delta MBH\)và \(\Delta NCH\)
\(\widehat{BMH}=\widehat{CNH}=90^o\)
\(BH=CH\left(cma\right)\)
\(\widehat{NBH}=\widehat{NQH}\)(Tam giác ABC cân tại A
\(\Rightarrow\Delta MBH=\Delta NCH\left(ch-gn\right)\)
\(MH=NH\left(2ctu\right)_{\left(1\right)}\)
Xét \(\Delta BQH\)và \(\Delta CNH\)
\(\widehat{Q}=\widehat{CNH}=90^o\)
\(BH=CH\left(cma\right)\)
\(\widehat{BHQ}=\widehat{NHC}\)(đối đỉnh)
\(\Rightarrow\Delta BQH=\Delta CNH\left(ch-gn\right)\)
\(\Rightarrow QH=NH\left(2ctu\right)_{\left(2\right)}\)
Từ \(\left(1\right),\left(2\right)\Rightarrow MH=QH\)
=> \(\Delta HQM\)cân tại H