Cho tam giác ABC nhọn, đường cao AH. Lấy điểm I bất kỳ trên cạnh AH. Qua I kẻ đường
thẳng song song với BC, cắt AB, AC lần lượt tại D, E.
a) Chứng minh: AI/AH=DE/BC
b) Cho
AI/AH=1/4
và diện tích tam giác ADE là 10 cm2
. Tính diện tích tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh =
Vì B’C’ // với BC => = (1)
Trong ∆ABH có BH’ // BH => = (2)
Từ 1 và 2 => =
b) B’C’ // BC mà AH ⊥ BC nên AH’ ⊥ B’C’ hay AH’ là đường cao của tam giác AB’C’.
Áp dụng kết quả câu a) ta có: AH’ = AH
= = => B’C’ = BC
=> SAB’C’= AH’.B’C’ = .AH.BC
=>SAB’C’= (AH.BC)
mà SABC= AH.BC = 67,5 cm2
Vậy SAB’C’= .67,5= 7,5 cm2

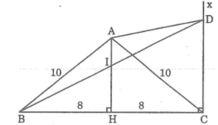
Áp dụng định lí Pi-ta-go vào tam giác vuông ABH ta có:
A B 2 = A H 2 + B H 2 ⇒ A H 2 = A B 2 - B H 2 = 10 2 - 8 2 = 36
Suy ra: AH = 6 (cm)
![]()
Suy ra: IH = AH – AI = 6 – 2 = 4 (cm)
Vì IH ⊥ BC và DC ⊥ BC nên IH // DC (1)
Mặt khác: BH = HC (gt) (2)
Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD
