Gọi O là trung điểm hay giao đ của BH và CK

là giao điểm phải ko bn @Trần Việt Linh

Xét ΔGBC và ΔHCB có 

GB=HC

\(\widehat{GBC}=\widehat{HCB}\)

BC chung

Do đó: ΔGBC=ΔHCB

Suy ra: \(\widehat{OCB}=\widehat{OBC}\)

hay ΔOBC cân tại O

ko đúng đề bạn êy

a) △ABC cân ⇒ \(\widehat{ABC}=\widehat{ACB}\) ⇒\(\widehat{ABM}=\widehat{ACN}\) 

Xét △ABM và △ACN có:

\(AB=AC\) ( Vì △ABC cân)

\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)

BM=CN(gt)

Do đó : △ABC=△ACN\(\left(c.g.c\right)\)

b)Xét △vuoongAHB và △vuoongAKC có

AB=AC(vì △ABC cân)

\(\widehat{HAB}=\widehat{KAC}\) (vì △ABM=△ACN)

⇒△AHB=△AKC ( cạnh huyền góc nhọn)

⇒AH=AK

a, Ta có : ^ABM = ^MBC - ^ABC (1) 

^ACN = ^NCB - ^ACB (2) 

Từ (1) ; (2) suy ra ^ABM = ^ACN 

Xét tam giác ABM và tam giác ANC có : 

^ABM = ^ANC ( cmt ) 

AB = AC ( gt )

MB = NC (gt)

Vậy tam giác ABM = tam  giác ACN ( c.g.c )

=> AM = AN ( 2 cạnh tương ứng )

Xét tam giác AMN có : AN = AM 

Vậy tam giác AMN là tam giác cân tại A 

=> ^M = ^N (3) 

b, Ta có : ^AMB = ^ABH ( cùng phụ ^HBM ) (4) 

^ACK = ^ANC ( cùng phụ ^KCN ) (5) 

Từ (3) ; (4) ; (5) suy ra : ^ABH = ^ACK 

=> ^HBM = ^KCN 

Xét tam giác AHB và tam giác AKC ta có : 

^ABH = ^ACK ( cmt )

AB = AC 

^AHB = ^AKC = 90⁰

Vậy tam giác AHB = tam giác AKC ( ch - gn )

=> AH = AK ( 2 cạnh tương ứng )

c, Ta có : ^HBM = ^OBC ( đối đỉnh ) 

^KCN = ^BCO ( đối đỉnh ) 

mà ^HBM = ^KCN (cmt) 

Xét tam giác OBC có : 

^OBC = ^OCB vậy tam giác OBC cân tại O

Lời giải:

a) Xét tam giác $ABH$ và $ACK$ có:

\(AB=AC\) (gt)

\(\widehat{A}\) chung

\(AK=AH\) (gt)

\(\Rightarrow \triangle ABH=\triangle ACK(c.g.c)\Rightarrow BH=CK\)

b)

Vì \(AB=AC; AK=AH\Rightarrow AB-AK=AC-AH\Rightarrow BK=CH\)

Từ tam giác bằng nhau phần a suy ra:

\(\widehat{ABH}=\widehat{ACK}\Leftrightarrow \widehat{KBO}=\widehat{HCO}\)

\(\widehat{AHB}=\widehat{AKC}\Rightarrow 180^0-\widehat{AHB}=180^0-\widehat{AKC}\)

\(\Rightarrow \widehat{CHO}=\widehat{BKO}\)

Xét tam giác $OKB$ và $OHC$ có:

\(KB=HC\) (cmt)

\(\widehat{OBK}=\widehat{OCH}\) (cmt)

\(\widehat{BKO}=\widehat{CHO}\) (cmt)

\(\Rightarrow \triangle OKB=\triangle OHC\) (g.c.g) (đpcm)

\(\Rightarrow OB=OC\)

c)

Xét tam giác $AOB$ và $AOC$ có:

\(\left\{\begin{matrix} OB=OC(cmt)\\ \text{OA chung}\\ AB=AC\end{matrix}\right.\Rightarrow \triangle AOB=\triangle AOC(c.c.c)\)

\(\widehat{OAB}=\widehat{OAC}\Rightarrow OA\) là phân giác góc $\widehat{BAC}$

Hình vẽ:

tam giác ABC cân tại A suy ra AB=AC và góc ABC = góc ACB

ta có \(\widehat{ABC}+\widehat{ABM}=180^o\\ \widehat{ACB}+\widehat{ACN}=180^o\)mà \(\widehat{ABC}=\widehat{ACB}\)\(\Rightarrow\widehat{ABM}=\widehat{ACN}\)

dễ thấy tam giác \(ABM=\Delta ACN\left(c.g.c\right)\)

suy ra AM = AN ( 2 cạnh tương ứng )

tam giác AMN có AM = AN suy ra tam giác AMN là tam giác cân

b) tam giác ABm = tam giác ACN suy ra góc MAB = góc NAC ( 2 góc tương ứng )

dễ thấy tam giác HBA = tam giác KCA ( cạnh huyền - góc nhọn )

suy ra BA = Ck ( 2 cạnh tương ứng ) 

c) \(\Delta AHK\)có AH=AK suy ra \(\Delta AHk\) là tam giác cân

\(\Delta AHK\)và  \(\Delta AMN\) có chung đỉnh

mà 2 tam giác này là 2 tam giác cân suy ra \(\widehat{AHK}=\widehat{AKH}=\widehat{AMN}=\widehat{ANM}\\ hay\widehat{AHK}=\widehat{AMN}\)

mà 2 góc này ở vị trí đồng vị bằng nhau suy ra HK//MN

d) kéo dài HB và CK cắt nhau tại O

nối AO

xét \(\Delta⊥AHO\)và \(\Delta⊥AKO\)có

AO là cạnh huyền chung

AH = AK

do đó \(\Delta AHO=\Delta AKO\) ( cạnh huyền - cạnh góc vuông )

e) xét tam giác \(BAD\)và \(\Delta CAD\)có

BA = CA ( tam giác ABC cân tại A )

DA = DC (gt)

AD là canh chung 

do đó \(\Delta BAD=\Delta CAD\left(c.c.c\right)\)

phù phù mệt quá còn mấy cái cuối gửi bn sau mk đi ngủ đã

tiếp nhé

suy ra góc BAD = góc CAD ( 2 góc tương ứng )

vì tia AD nằm giữa 2 tia AB và AC nên AD là phân giác góc BAC (1)

ta có BH = CK ( cmt)

và HO = KO (cmt)

suy ra HO-HB=OK-CK ( vì B nằm giữa H và O , C nằm giữa O và K )

hay BO = OC

xét \(\Delta BAO\)và \(\Delta CAO\)có \(\hept{\begin{cases}AOchung\\BO=OC\left(cmt\right)\\BA=CA\left(gt\right)\end{cases}}\)

do đó \(\Delta BAO=\Delta CAO\left(c.c.c\right)\)

suy ra góc BAO = góc CAO ( 2 góc tương ứng )

vì tia AO nằm giữa 2 tia AB và AC suy ra AO là phân giác góc BAC (2)

từ (1) và (2) suy ra A;D;O thẳng hàng 

a) Ta có: AK+KB=AB(K nằm giữa A và B)

AH+HC=AC(H nằm giữa A và C)

mà AK=AH(gt)

và AB=AC(ΔABC cân tại A)

nên KB=HC

Xét ΔKBC và ΔHCB có 

KB=HC(cmt)

\(\widehat{KBC}=\widehat{HCB}\)(hai góc ở đáy của ΔABC cân tại A)

BC chung

Do đó: ΔKBC=ΔHCB(c-g-c)

Suy ra: \(\widehat{KCB}=\widehat{HBC}\)(hai góc tương ứng)

hay \(\widehat{OBC}=\widehat{OCB}\)

Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)

nên ΔOBC cân tại O(Định lí đảo của tam giác cân)

b) Xét ΔAKH có AK=AH(gt)

nên ΔAKH cân tại A(Định nghĩa tam giác cân)

Ta có: ΔAKH cân tại A(cmt)

nên \(\widehat{AKH}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAKH cân tại A)(1)

Ta có: ΔABC cân tại A(gt)

nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)

Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)

mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị

nên KH//BC(Dấu hiệu nhận biết hai đường thẳng song song)

Thanks kiu bạn

+) Xét ΔABH và ΔACK, ta có:

AB = AC ( vì tam giác ABC cân tại A)

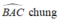
AH = AK (giả thiết)

Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.

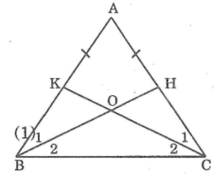
Hình vẽ:

Giải:

Xét \(\Delta ABH\) và \(\Delta ACK\) có:

\(AH=AK\left(gt\right)\)

\(\widehat{A}\) là góc chung

\(AB=AC\) ( Vì \(\Delta ABC\) cân tại \(A\) )

Do đó: \(\Delta ABH=\Delta ACK\left(c.g.c\right)\)

\(\Rightarrow\widehat{B_2}=\widehat{C_2}\) ( cặp góc tương ứng )

Mà \(\widehat{B}=\widehat{C}\) ( Do \(\Delta ABC\) cân tại \(A\) )

\(\Rightarrow\widehat{B}-\widehat{B_2}=\widehat{C}-\widehat{C_2}\)

\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)

\(\Rightarrow\Delta OBC\) cân tại \(O\) . \(\left(đpcm\right)\)

a: Xét ΔABH và ΔACK có 

AB=AC

\(\widehat{A}\) chung

AH=AK

Do đó: ΔABH=ΔACK

Xét ΔAHB và ΔAKC có:

 AB=AC(gt)

A^ : góc chung

AH=AK(gt)

=>ΔAHB=ΔAKC(c.g.c)

=>ˆABH=ˆACK

Có: ˆB=ˆABH+ˆCBH

      ˆC=ˆACK+ˆBCK

Mà ˆB=ˆC(gt);^ABH=ˆACK(cmt)

=> ˆCBH=ˆBCK

=>ΔOBC cân tại O