2 vật có khối lượng m1 và m2 (với m1 > m2) đang chuyển động và có động năng bằng nhau. So sánh vận tốc của 2 vật?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
27 tháng 2 2021
Ta có: \(W_{đ1}=\dfrac{1}{2}m_1v^2\) (1)
và \(W_{đ2}=\dfrac{1}{2}m_2v^2=\dfrac{1}{2}.2.m_1v^2=m_1v^2\) (2)
Từ (1),(2) => \(\dfrac{W_{đ1}}{W_{đ2}}=\dfrac{1}{2}\Rightarrow W_{đ1}=\dfrac{1}{2}W_{đ2}\)
AM
7 tháng 2 2022
Xét hệ kín, bảo toàn động lượng ta có: \(m_1v_1-m_2v_2=\left(m_1+m_2\right)v\)
\(\Leftrightarrow0,5.4-0,3.2=\left(0,5+0,3\right)v\)
\(\Leftrightarrow v=1,75\) m/s
Sau va chạm cả hai chuyển động cùng chiều với vật thứ nhất
7 tháng 2 2022
Động lượng vật 1:
\(p_1=m_1\cdot v_1=0,5\cdot4=2kg.m\)/s
Động lượng vật 2:
\(p_2=m_2\cdot v_2=0,5\cdot2=1kg.m\)/s
Hai vật cđ ngược chiều bảo toàn động lượng:
\(m_1\cdot v_1-m_2\cdot v_2=\left(m_1+m_2\right)\cdot v\)
\(\Rightarrow2-1=\left(0,5+0,5\right)\cdot v\)
\(\Rightarrow v=1\)m/s
VT
7 tháng 10 2019
Chọn đáp án C
? Lời giải:
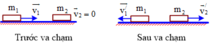
+ Chọn chiều dương là chiều chuyển động ban đầu của m1.
6 tháng 2 2021
Ta có : \(\left\{{}\begin{matrix}\overrightarrow{P_1}=m_1\overrightarrow{v_1}=2\overrightarrow{v_1}\\\overrightarrow{P_2}=m_2\overrightarrow{v_2}=3\overrightarrow{v_2}\end{matrix}\right.\)
Có : \(P=\sqrt{P_1^2+P_2^2+2P_1P_2Cos\left(\overrightarrow{P_1};\overrightarrow{P_2}\right)}\)
Lại có : Vecto P1 và P2 cùng phương với v1 và v2
Và \(\overrightarrow{v_1}.\overrightarrow{v_2}=v_1.v_2.cos\left(\overrightarrow{v1};\overrightarrow{v2}\right)\)
=> \(\left(\overrightarrow{P1};\overrightarrow{P2}\right)=45^o\)
\(\Rightarrow P=\sqrt{4v_1^2+9v^2_2+2.2.3\overrightarrow{v_1}\overrightarrow{v_2}.Cos45}=6\sqrt{7}\left(\dfrac{Kg.m}{s}\right)\)
19 tháng 4 2023
6 căn 7 mik bấm ra 15,8 trong khi đó mik tính lại lại ra 16,8 cơ
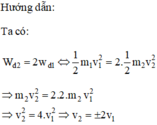
Tóm tắt :
m1 > m2
A1=A2
So sánh V1 và V2
Giải
Ta có A1 =P1.s=10.m1.V1.t
A2 = P2.s=10.m2.V2.t
vì A1=A2 nên 10.m1.V1.t =10.m2.V2.t
=> m1.V1=m2.V2
mà m1> m2
=> V1 < V2
Vậy ...