chứng minh nếu một đường thẳng cắt một trong hai đường thẳng song song thì sẽ cắt đường thẳng còn lại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2020
a đương nhiên sẽ cắt b nếu không cắt thì không có đường thẳng song song :)))
HC
0
29 tháng 12 2023
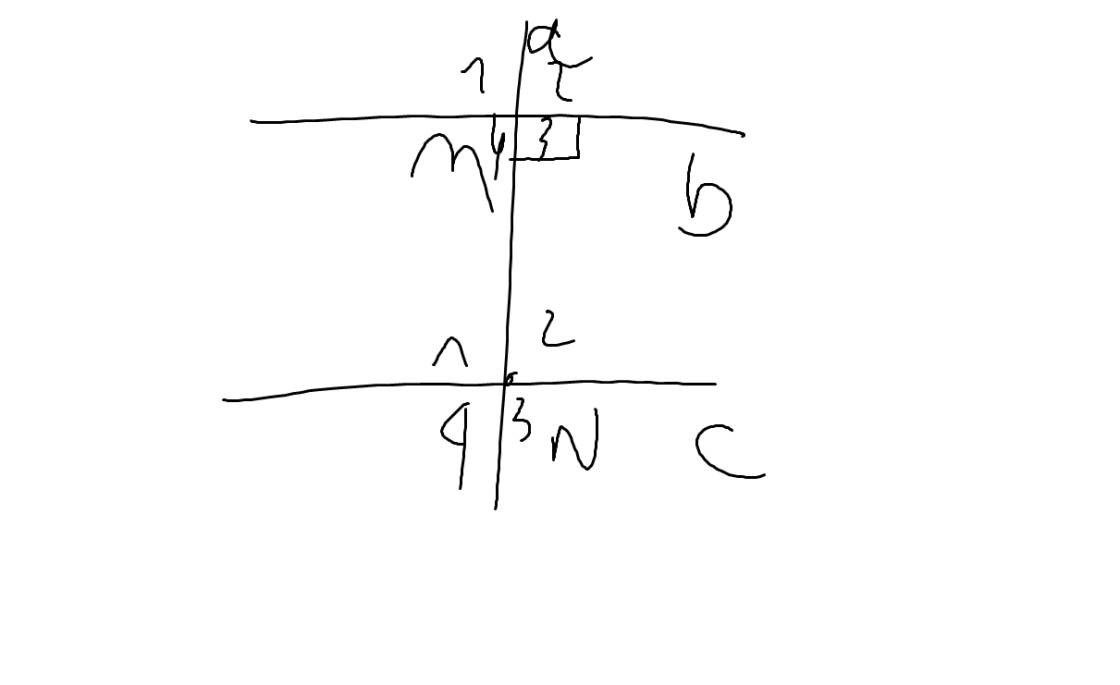
| GT | a\(\perp\)b tại M a cắt c tại N b//c |
| KL | a\(\perp\)c tại N |
Chứng minh định lí:
Ta có: b//c
=>\(\widehat{M_3}=\widehat{N_1}\)(hai góc so le trong)
mà \(\widehat{M_3}=90^0\)
nên \(\widehat{N_1}=90^0\)
=>a\(\perp\)c tại N
23 tháng 10 2015
Ta có: a // b => E = I (hai góc so le trong)
Mà: E1 = \(\frac{E}{2}\)
I1 = \(\frac{I}{2}\)
=> E1 = E1 và có vị trí so le trong => m // n
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song. (Dấu hiệu nhận biết hai đường thẳng song song)
b) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau
PT
5 tháng 11 2020
theo dinh li py ta goco 1 cap goc trong cung phia bu nhau 90 do thi 2 duong thang do song song
DN
15 tháng 11 2017
Từ t/c :
Nếu đường thẳng a và đường thẳng b cùng vuông góc với 1 đường thẳng thì hai đường thẳng a và đường thẳng b song song với nhau.
=> đpcm.
dâm dê