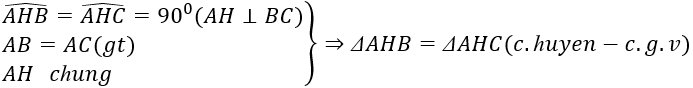Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC( H thuộc BC). Tính độ dài AH biết HB=2 cm, HC=8 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


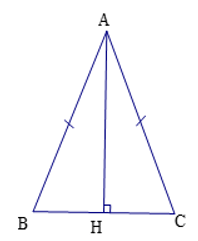
cho tam giác ABC cân tại A, kẻ AH vuông góc BC ( H thuộc BC )
a) CHỨNG MINH GÓC BAH = GÓC CEB
b) CHO AH= 3 cm , BC= 8 cm . TÍNH ĐỘ DÀI AC
c) KẺ HE VUÔNG GÓC AB , HD VUÔNG GÓC AC , CHỨNG MINH AE=AD
d) CHỨNG MINH ED SONG SONG BC
trả lời :
Xét \(\Delta\)ABC vuông tại A , có:
AH là đường cao (H\(\in\)BC)
Ta lại có: BC = HB + HC = 2 + 8 = 10 (cm) (1)
\(\Delta\)ABC vuông tại A
=> BC là cạnh huyền (2)
Từ (1) và (2) => AH = \(\frac{1}{2}\)BC = 4(cm)

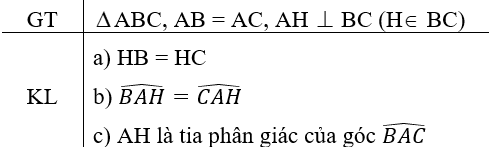
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: BH=CH=12/2=6cm
=>AC=căn AH^2+HC^2=10cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H

:
a)Vì △ABC cân tại A nên AH là đg cao đồng thời cx là đg p/g, đường trung tuyến.
HB=HC và BAHˆ=CAHˆ
b)HC=BC2=82=4
Áp dụng định lý Py-ta-go vào tam gíác vuông AHC có:
AH2=AC2−HC2=.......
AH=...........
c)Xét 2 tam gíác vuông : BDH và CEH có
HB=HC(cmt)
Bˆ=Cˆ(△ABC cân)
Do đó: △BDH=△CEH
DH =EH
dpcm
Bài 3 :
a)Vì △ABC cân tại A nên AH là đg cao đồng thời cx là đg p/g, đường trung tuyến.
HB=HC và BAHˆ=CAHˆ
b)HC=BC2=82=4
Áp dụng định lý Py-ta-go vào tam gíác vuông AHC có:
AH2=AC2−HC2=.......
AH=...........
c)Xét 2 tam gíác vuông : BDH và CEH có
HB=HC(cmt)
Bˆ=Cˆ(△ABC cân)
Do đó: △BDH=△CEH
DH =EH
dpcm

+) +) Xét Δ ABH vuông tại H
\(\Rightarrow AB^2=AH^2+BH^2\) ( định lí Py-ta-go )
\(\Rightarrow AB^2=4^2+2^2\)
\(\Rightarrow AB^2=16+4=20\)
\(\Rightarrow AB=\sqrt{20}\) ( do AB > 0 )
+) Xét Δ AHC vuông tại H
\(\Rightarrow AC^2=AH^2+HC^2\) ( định lí Py-ta-go)
\(\Rightarrow AC^2=4^2+8^2\)
\(\Rightarrow AC^2=16+64=80\)
\(\Rightarrow AC=\sqrt{80}\) ( do AC > 0 )
+) Ta có \(AH\perp BC\) tại H
\(\Rightarrow H\in BC\)
\(\Rightarrow\) HB + HC = BC
=> BC = 2 + 8 = 10 ( cm)
Vậy ...
@@ Học tốt
Đề bài nó cho số k đẹp hay là t tính sai nhỉ ?

a, Xét \(\Delta ABH\) và\(\Delta ACH\) CÓ:
\(AHchung\)
AB = AC
\(\widehat{AHB}=\widehat{AHC}\)
\(\Rightarrow\Delta ABH=\Delta ACH\)(cạnh huyền cạnh góc vuông)
=> BH = HC ( 2 cạnh tương ứng )
b,Do BC = 8cm => BH = 4cm
Áp dụng định lý Py ta go vào tam giác vuông ABH có :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH^2=AB^2-BH^2\)\(\Rightarrow AH^2=5^2-4^2=25-16=9\)\(\Rightarrow AH=3\left(cm\right)\)
c,\(Xét\Delta DBH\) và\(\Delta ECH\) có :
\(\widehat{ABH}=\widehat{ACH}\)
BH = HC
\(\widehat{BDH}=\widehat{CEH}\)
\(\Rightarrow\Delta DBH=\Delta ECH\)\(\Rightarrow DH=EH\)=> \(\Delta DHE\) cân tại H
cho mình 1 tym nha

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
b: Ta có: HB=HC
H nằm giữa B và C
Do đó: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=4\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-4^2=9\)
=>\(AH=\sqrt{9}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H

a.ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến => HB = HC
b.áp dụng định lý pitago ta có:
\(AB^2=AH^2+HB^2\)
\(5^2=AH^2+\left(8:2\right)^2\)
\(AH=\sqrt{5^2-4^2}=3cm\)
c.Xét tam giác vuông BHD và tam giác vuông CHE, có:
BH = CH ( cmt )
góc B = góc C ( ABC cân )
Vậy tam giác vuông BHD = tam giác vuông CHE
=> HD = HE
=> HDE cân tại H
d.ta có AB = AD + DB
AC = AE + EC
Mà BD = CE ( 2 cạnh tương ứng của 2 tam giác bằng nhau )
=> AD = AE
=> ADE cân tại A
Mà A là đường cao cũng là đường trung trực trong tam giác cân ABC cũng là đường trung trực của tam giác cân ADE ( cmx )
Chúc bạn học tốt !!!!