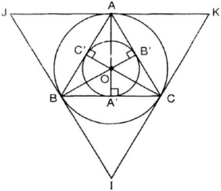
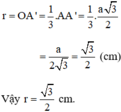Cho tam giác đều ABC nội tiếp (O;R). Lấy điểm M bất kì trên cung nhỏ BC (M không trùng với B,C).Đường thẳng kẻ qua A vuông góc với CM tại H cắt tia BM tại K
a)Chứng minh H là trung điểm AK
b)Chứng minh K luôn nằm trên 1 đường tròn cố định khi M thay đổi.Tính bán kính đường tròn đó biết R=\(3\sqrt{3}\)
c)Gọi D là giao của AM và BC.Tìm vị trí điểm M sao cho tích 2 bán kính của đường tròn ngoại tiếp của 2 tam giác MBD,MCD đạt giá trị lớn nhất