gggggggggggggggggggggggggggg

a: Xét ΔDEF có DI là phân giác

nên \(\dfrac{DE}{DF}=\dfrac{EI}{IF}\)

=>\(\dfrac{EI}{4,8}=\dfrac{10}{6}=\dfrac{5}{3}\)

=>EI=8(cm)

b: Ta có: EI+IF=EF

=>EF=6+8=14(cm)

Xét ΔEDF có MI//DF

nên \(\dfrac{MI}{DF}=\dfrac{EI}{EF}=\dfrac{EM}{ED}\)

=>\(\dfrac{MI}{6}=\dfrac{EM}{10}=\dfrac{6}{14}=\dfrac{3}{7}\)

=>\(MI=\dfrac{18}{7}\left(cm\right);EM=\dfrac{30}{7}\left(cm\right)\)

MD+ME=DE

=>MD+30/7=10

=>MD=40/7(cm)

c: Xét ΔDEF có DI là phân giác

nên \(\dfrac{EI}{IF}=\dfrac{ED}{DF}\left(1\right)\)

Xét ΔEDF có MI//DF

nên \(\dfrac{EI}{IF}=\dfrac{ME}{MD}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{ED}{DF}=\dfrac{ME}{MD}\)

`@` `\text {dnammv}`

`a,`

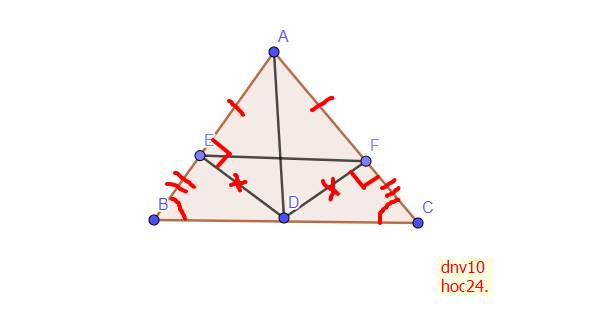
Xét \(\Delta BED\) và \(\Delta CFD\) có:

\(\left\{{}\begin{matrix}\text{BD = CD (D là trung điểm của BC}\\\widehat{\text{B}}=\widehat{\text{C}}\left(\text{ }\Delta\text{ABC cân tại A}\right)\\\widehat{BED}=\widehat{CFD}\left(=90^0\right)\end{matrix}\right.\)

`=> \Delta BED = \Delta CFD (ch-gn)`

`-> \text {BE = CF (2 cạnh tương ứng)}`

`b,`

Vì `\Delta BED = \Delta CFD (a)`

`-> \text {DE = DF (2 cạnh tương ứng)}`

`\text {Xét}` `\Delta DEF:`

`\text {DE = DF}`

`-> \Delta DEF` là `\Delta` cân

`c,`

Vì \(\left\{{}\begin{matrix}\text{AB = AC (tam giác ABC cân tại A)}\\\text{BE = CF (a)}\end{matrix}\right.\)

`-> \text {AE = AF}`

\(\text{Xét }\Delta\text{ AEF}: \)

`\text {AE = AF}`

`-> \Delta AEF` là `\Delta` cân (tại A).

`->`\(\widehat {AEF}= \widehat {AFE}\)\(=\dfrac{180-\widehat{A}}{2}\text{ }\left(1\right)\)

`\Delta ABC` cân tại `A`

`->`\(\widehat {ABC}= \widehat {ACB}=\)\(\dfrac{180-\widehat{A}}{2}\text{ }\left(2\right)\)

Từ `(1)` và `(2)`

`->`\(\widehat {AEF}= \widehat {ABC}\)

Mà `2` góc này nằm ở vị trí đồng vị

`-> \text {EF // BC (tính chất 2 đường thẳng //).}`

a) Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:

\(EF^2=DE^2+DF^2\)

\(\Leftrightarrow EF^2=9^2+12^2=225\)

hay EF=15(cm)

Vậy: EF=15cm

a) Xét tam giác EDF có: _EF² = _{DE^{2 +} DF²} (đ/lí py-ta-go)

                                         =>  EF² = 9² + 12²

                                                 =>  EF² = 81 + 144 = 225

                                         =>  EF = 112,5 cm

tu  ve hinh :

cau b la vuong goc phai k

a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)

goc ADB = goc ADC do AD | BC (GT)

=> tamgiac ADB = tamgiac ADC (ch - gn)

=> BD = DC (dn)

b, xet tamgiac BHD va tamgiac CKD co :  BD = DC (Cau a)

goc ABC = goc ACB (cau a)

goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)

=> tamgiac BHD = tamgiac CKD (ch - gn)

=> HD = DK (dn)

c, xet tamgiac AHD va tamgiac AKD co : AD chung

HD = DK (cau b) 

goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt) 

=> tamgiac AHD = tamgiac AKD  (ch - cgv)

=> tamgiac AHK can tai A (dn)

=> goc AHK = (180 - goc BAC) : 2

tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2

=> goc AHK = goc ABC  2 goc nay dong vi

=> HK // BC (tc)

d, tu ap dung py-ta-go 

bài 2 nữa ạ

Mình làm phần d) thôi nhé!

Theo phần a) ta có được: \(\widehat{AIB}=\widehat{AIC}\)(2 góc tương ứng:

Tam giác ABI = Tam giác ACI)

mà \(\widehat{AIB}+\widehat{AIC}=180\)(2 góc kề bù)

=>\(\widehat{AIB}=\widehat{AIC}=90\)

Xét tam giác ABI vuông tại I, áp dụng định lí py-ta-go ta có:

\(AB^2=AI^2+BI^2\)(1)

Xét tam giác ADI vuông tại D, áp dụng định lí py-ta-go ta có:

\(AI^2=AD^2+DI^2\)(2)

Xét tam giác BDI vuông tại D, áp dụng định lí py-ta-go ta có:

\(BI^2=DI^2+BD^2\)(3)

Thay (2),(3) vào (1) ta có được:

\(AB^2=AD^2+DI^2+DI^2+BD^2\)

(hay) \(AB^2=AD^2+BD^2+2DI^2\)(ĐPCM)