Gọi I là tâm đường tròn tâm C (x-1)^2+(y-1)^2=4.Tổng giá trị của m để đường thẳng x+y-m=0 cắt đường tròn(C) tại hai điểm phân biệt A,B sao cho IAB có diện tích lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)
a. Đường thẳng cắt đường tròn tại 2 điểm pb khi:
\(d\left(I;d\right)< R\Leftrightarrow\dfrac{\left|\sqrt{2}-2m+1-\sqrt{2}\right|}{\sqrt{2+m^2}}< 3\)
\(\Leftrightarrow\left(2m-1\right)^2< 9\left(m^2+2\right)\)
\(\Leftrightarrow8m^2+4m+17>0\) (luôn đúng)
Vậy đường thẳng luôn cắt đường tròn tại 2 điểm pb với mọi m
b. \(S_{IAB}=\dfrac{1}{2}IA.IB.sin\widehat{AIB}=\dfrac{1}{2}R^2.sin\widehat{AIB}\le\dfrac{1}{2}R^2\) do \(sin\widehat{AIB}\le1\)
Dấu "=" xảy ra khi \(sin\widehat{AIB}=1\Rightarrow\Delta IAB\) vuông cân tại I
\(\Rightarrow d\left(I;d\right)=\dfrac{R}{\sqrt{2}}\Leftrightarrow\dfrac{\left|2m-1\right|}{\sqrt{m^2+2}}=\dfrac{3}{\sqrt{2}}\)
\(\Leftrightarrow m^2+8m+16=0\Rightarrow m=-4\)

Chọn C
![]() .
.
Vì ![]() nên phương trình
nên phương trình ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị ![]() .
.
Giả sử hàm số có hai điểm cực trị lần lượt là ![]() và
và ![]() , với
, với ![]() ,
, ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]() .
.
Thực hiện phép chia ![]() cho
cho ![]() ta được :
ta được : ![]() .
.
Khi đó ta có: 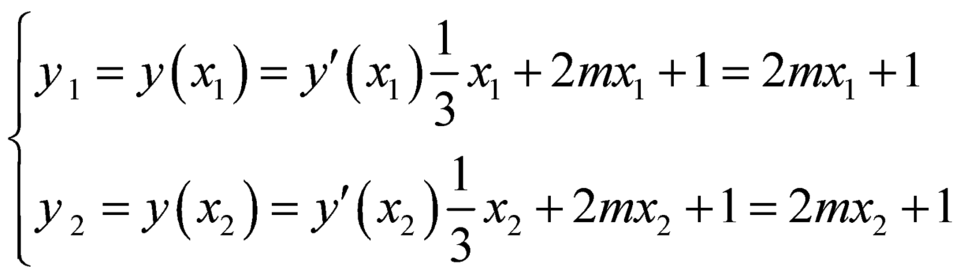 .
.
Ta thấy, toạ độ hai điểm ![]() và
và ![]() thoả mãn phương trình
thoả mãn phương trình ![]() .
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là ![]() .
.
Ta thấy ![]() luôn qua
luôn qua ![]() .
.
Đặt ![]()
![]() .
.
![]() .
.
Xét hàm số ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Suy ra hàm số ![]() liên tục và đồng biến trên
liên tục và đồng biến trên ![]() .
.
Do đó ![]() .
.
Vậy ![]() đạt giá trị lớn nhất
đạt giá trị lớn nhất ![]()
![]() .
.
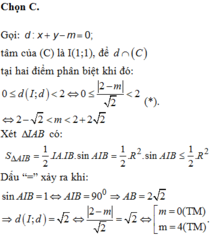






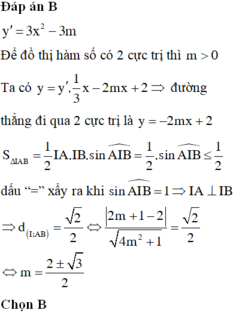
\(I\left(1;1\right)\) , bán kính \(R=2\)
Do \(sin\widehat{AIB}\le1\Rightarrow S_{IAB}=\frac{1}{2}IA.IB.sin\widehat{AIB}\le\frac{1}{2}IA.IB=\frac{1}{2}R^2=2\)
\(\Rightarrow S_{max}=2\) khi \(\widehat{AIB}=90^0\)
Gọi H là hình chiếu của I lên AB, áp dụng hệ thức lượng cho tam giác vuông AIB:
\(\frac{1}{IH^2}=\frac{1}{IA^2}+\frac{1}{IB^2}=\frac{2}{R^2}\Rightarrow IH=\frac{R}{\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow d\left(I;AB\right)=\sqrt{2}=\frac{\left|1+1-m\right|}{\sqrt{1^2+1^2}}\Rightarrow\left|2-m\right|=2\Rightarrow\left[{}\begin{matrix}m=0\\m=4\end{matrix}\right.\)