Cho tam giác ABC vuông tạiA (AB < AC). Gọi O là trung điểm của BC. Trên tia đối của tia OA lấy điểm E sao cho OE = OA.Chứng minh tứ giác ACEB là hình chữ nhật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác ABEC có
O là trung điểm của BC
O là trung điểm của AE
Do đó: ABEC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABEC là hình chữ nhật

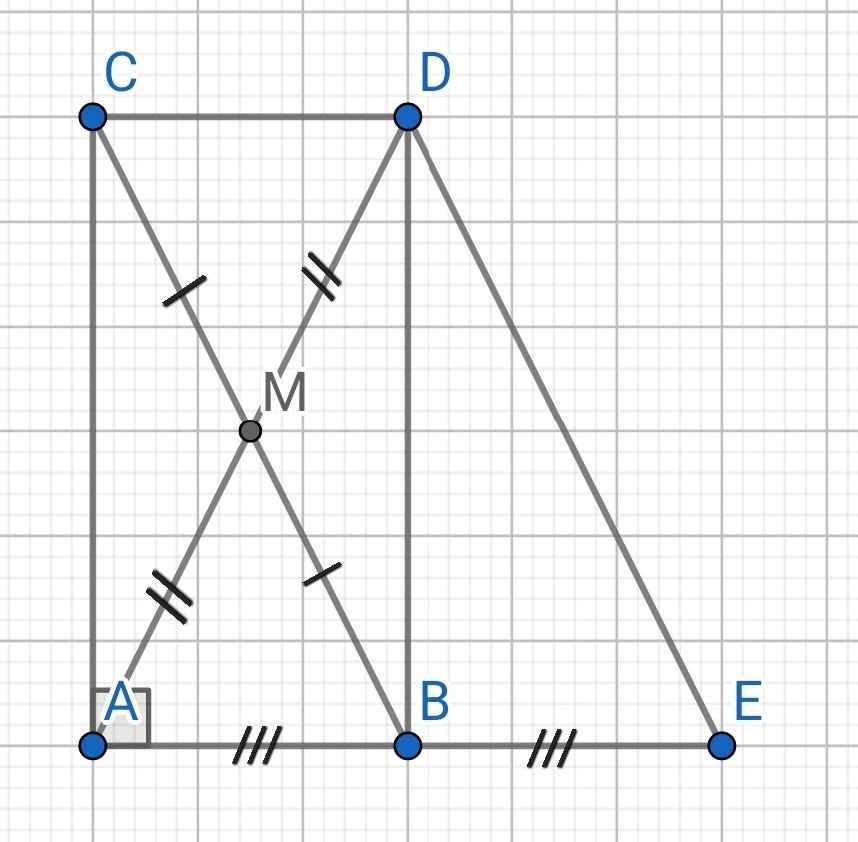 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!

Xét tứ giác ABDC có
O là trung điểm của BC
O là trung điểm của AD
Do đó: ABDC là hình bình hành

a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành

a: Xét tứ giác ABNC có
O là trung điểm chung của AN và BC
=>ABNC là hình bình hành
Hình bình hành ABNC có \(\widehat{BAC}=90^0\)
nên ABNC là hình chữ nhật
b: CN//AB
\(C\in\)DN
Do đó: CD//AB
CN=AB
CN=CD
Do đó: AB=CD
Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành

a: Xét tứ giác AHBD có
O là trung điểm chung của AB và HD
=>AHBD là hình bình hành
Hình bình hành AHBD có \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật
b: Ta có: AHBD là hình chữ nhật
=>AH//BD và AH=BD
Ta có: AH//BD
Q\(\in\)AH
Do đó: QH//DB
Ta có: AH=BD
AH=HQ
Do đó: BD=HQ
Xét tứ giác BDHQ có
BD//HQ
BD=HQ
Do đó: BDHQ là hình bình hành
c: Xét tứ giác ABQP có
H là trung điểm chung của AQ và BP
=>ABQP là hình bình hành
Hình bình hành ABQP có AQ\(\perp\)BP
nên ABQP là hình thoi
d: Ta có: ΔKAB vuông tại K
mà KO là đường trung tuyến
nên \(KO=\dfrac{AB}{2}\)
mà AB=HD(AHBD là hình chữ nhật)
nên \(KO=\dfrac{HD}{2}\)
Xét ΔKHD có
KO là đường trung tuyến
\(KO=\dfrac{HD}{2}\)
Do đó: ΔKHD vuông tại K
=>KH\(\perp\)KD

\(a,\) Vì M là trung điểm AB cà DH nên AHBD là hình bình hành
Mà \(\widehat{AHB}=90^0\) (đường cao AH) nên AHBD là hcn
\(b,\) Vì AHBD là hcn nên \(AD=BH;AD\text{//}HB\)
Mà \(BH=HE\Rightarrow AD=HE;AD\text{//}HE\)
Do đó: ADHE là hình bình hành
\(c,\) Vì ADHE là hbh mà N là giao AH và DE nên N là trung điểm AH và DE
Mà M là trung điểm AB nên MN là đtb \(\Delta ABH\)
Do đó \(MN//BH\) hay \(MN//BC\)
Ta có N là trung điểm AH và K là trung điểm AC nên NK là đtb \(\Delta ACH\)
Do đó \(NK//HC\) hay \(NK//BC\)
Do đó theo định lí Ta lét thì MN trùng NK hay M,N,K thẳng hàng
a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật


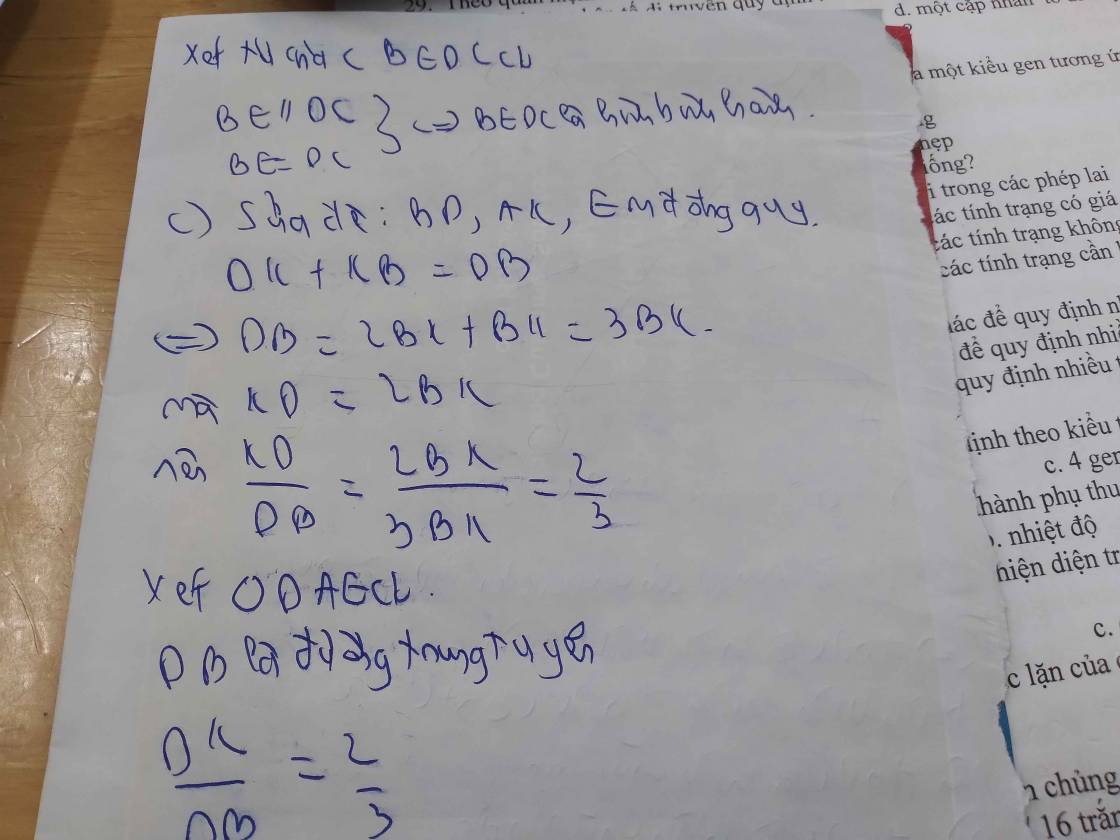

Mng trl giúp e vs ạ
Xét tứ giác ACEB có
O là trung điểm của AE
O là trung điểm của BC
Do đó: ACEB là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ACEB là hình chữ nhật