Vẽ đồ thị hàm số bậc hai, lập bảng biến thiên, tìm khoảng đồng biến, nghịch biến
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
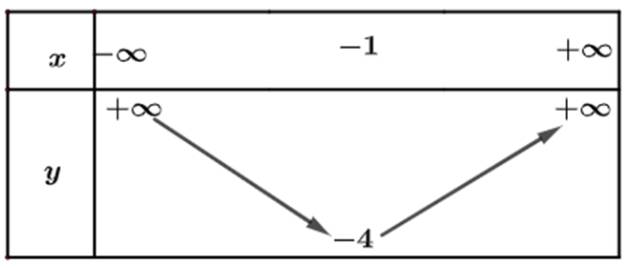
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
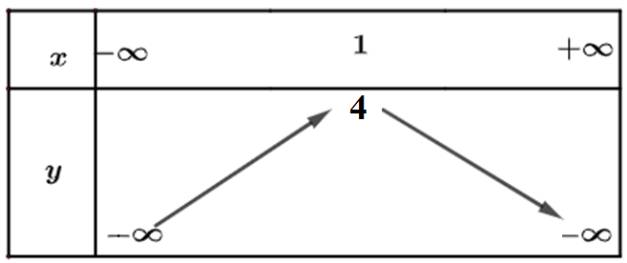

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3

a: 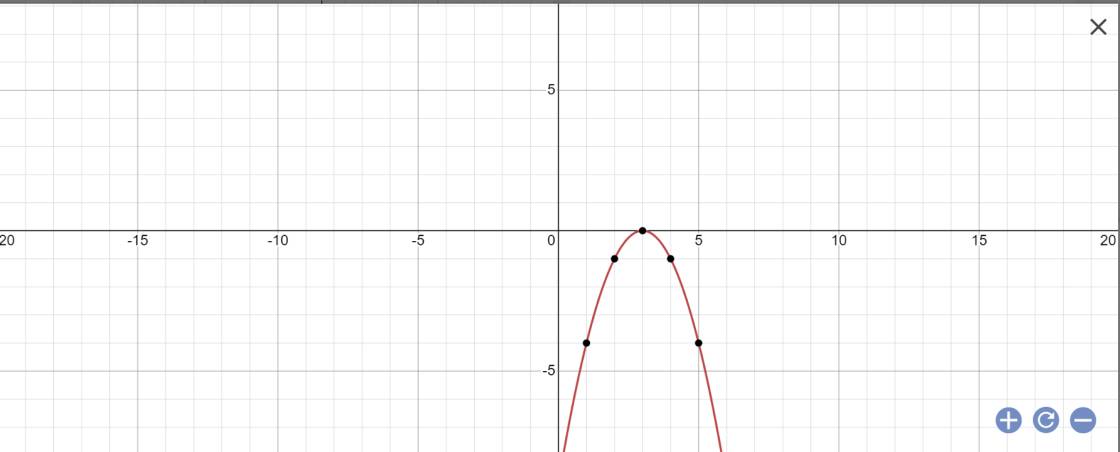
Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot\left(-1\right)}=\dfrac{6}{2}=3\\y=-\dfrac{6^2-4\cdot\left(-1\right)\cdot\left(-9\right)}{4\cdot\left(-1\right)}=0\end{matrix}\right.\)
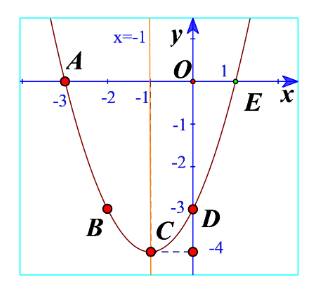
=>Hàm số đồng biến khi x<3 và nghịch biến khi x>3
b: 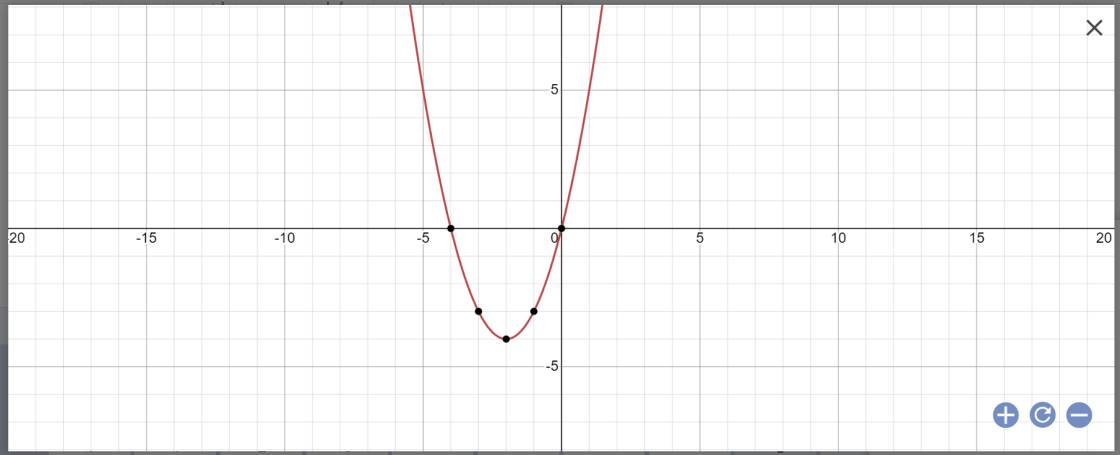
Tọa độ đỉnh là I(-2;-4)
=>Hàm số đồng biến khi x>-2 và nghịch biến khi x<-2

Bảng biến thiên
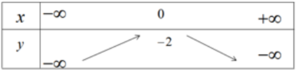
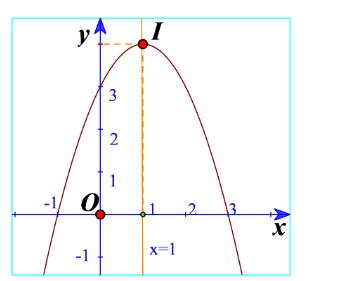
Hàm số đồng biến trên khoảng ( - ∞ ; 0 ) nghịch biến trên khoảng ( 0 ; + ∞ ) , hàm số là chẵn.
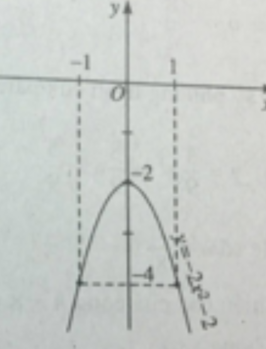
Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4).
Đồ thị hàm số y = - 2 ( x 2 + 1 ) được vẽ trên hình 38.

Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;
![]()
Vì a > 0, ta có bảng biến thiên
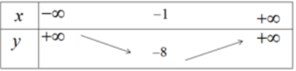
Hàm số nghịch biến trên khoảng (-∞; -1) đồng biến trên khoảng (-1; +∞)
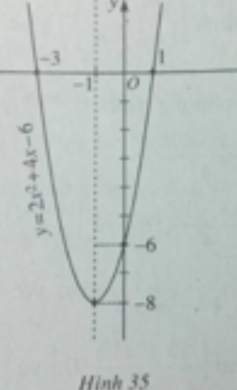
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).
Đồ thị của hàm số y = 2 x 2 + 4 x - 6 được vẽ trên hình 35.

Bảng biến thiên
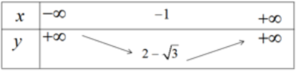
Hàm số nghịch biến trên khoảng ( - ∞ ; - 1 ) đồng biến trên khoảng ( - 1 ; + ∞ )
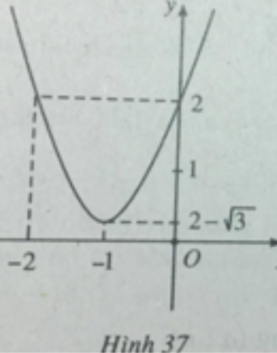
Đỉnh parabol ( - 1 ; 2 - 3 )
Đồ thị hàm số được vẽ trên hình 37.

Bảng biến thiên
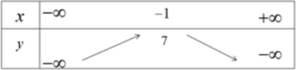
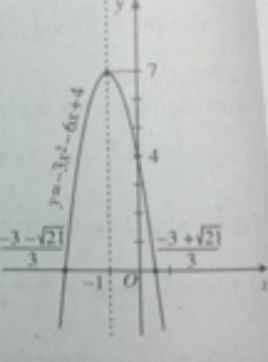
Hàm số đồng biến trên khoảng (-∞; -1) nghịch biến trên khoảng (-1; +∞)
Đỉnh parabol I(-1;7). Đồ thị của hàm số y = - 3 x 2 - 6 x + 4 được vẽ trên hình 36.