TK

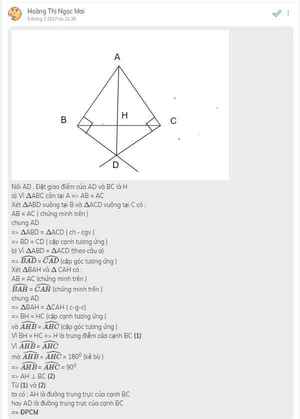
Nguồn: Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc vs AB, qua C kẻ đường thẳng vuông góc vsAC, 2 đường thẳng cắt nhau ở D, chứng minh: a, BD=CD B,Đường thẳng AD là dường trung trực của BC - Hoc24

???

đề đúng mà

a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC

Ta có: O nằm trên đường trung trực của AB(gt)

mà OG⊥AB(gt)

nên G là trung điểm của AB

Ta có: O nằm trên đường trung trực của AC(gt)

mà OF⊥AC(gt)

nên F là trung điểm của AC

Ta có: \(AG=\dfrac{AB}{2}\)(G là trung điểm của AB)

\(AF=\dfrac{AC}{2}\)(F là trung điểm của AC)

mà AB=AC(ΔABC cân tại A)

nên AG=AF

Xét ΔAGO vuông tại G và ΔAFO vuông tại F có 

AO chung

AG=AF(cmt)

Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)

Suy ra: \(\widehat{GAO}=\widehat{FAO}\)(hai góc tương ứng)

hay \(\widehat{BAO}=\widehat{CAO}\)

mà tia AO nằm giữa hai tia AB,AC

nên AO là tia phân giác của \(\widehat{BAC}\)(đpcm)

c) Xét ΔAOB và ΔAOC có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAO}=\widehat{CAO}\)(cmt)

AO chung

Do đó: ΔAOB=ΔAOC(c-g-c)

Suy ra: OB=OC(hai cạnh tương ứng)

Ta có: \(\widehat{ABC}+\widehat{KBC}=\widehat{ABK}\)(tia BC nằm giữa hai tia BA,BK)

nên \(\widehat{ABC}+\widehat{KBC}=90^0\)(1)

Ta có: \(\widehat{ACB}+\widehat{KCB}=\widehat{ACK}\)(tia CB nằm giữa hai tia CA,CK)

nên \(\widehat{ACB}+\widehat{KCB}=90^0\)(2)

Từ (1) và (2) suy ra \(\widehat{ABC}+\widehat{KBC}=\widehat{ACB}+\widehat{KCB}\)

mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)

nên \(\widehat{KBC}=\widehat{KCB}\)

Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)(cmt)

nên ΔKBC cân tại K(Định lí đảo của tam giác cân)

Suy ra: KB=KC(hai cạnh bên)

Xét ΔBEC vuông tại E và ΔCDB vuông tại D có 

BC chung

\(\widehat{EBC}=\widehat{DCB}\)(hai góc ở đáy của ΔABC cân tại A)

Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)

Suy ra: \(\widehat{BCE}=\widehat{CBD}\)(hai góc tương ứng)

hay \(\widehat{HBC}=\widehat{HCB}\)

Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)(cmt)

nên ΔHBC cân tại H(Định lí đảo của tam giác cân)

Suy ra: HB=HC(hai cạnh bên)

Ta có: AB=AC(ΔABC cân tại A)

nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)

Ta có: OB=OC(cmt)

nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)

Ta có: HB=HC(cmt)

nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)

Ta có: KB=KC(cmt)

nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)

Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)

Nhật Tân

p/s: kham khảo

Xét ΔABM vuông tại B và ΔACM vuông tại C có 

AM chung

AB=AC(ΔABC cân tại A)

Do đó: ΔABM=ΔACM(cạnh huyền-cạnh góc vuông)

Suy ra: BM=CM(hai cạnh tương ứng)

Ta có: AB=AC(ΔABC cân tại A)

nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: BM=CM(cmt)

nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)

Từ (1) và (2) suy ra AM là đường trung trực của BC

a) Gọi I là giao điểm của AM và BC

Xét \(\Delta ABM\) vuông tại B và \(\Delta ACM\) vuông tại C có :

AB =AC ( \(\Delta ABC\) cân tại A )

Cạnh AM chung

\(\Rightarrow\Delta ABM=\Delta ACM\) ( cạnh huyền - cạnh góc vuông )

\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) ( 2 góc tương ứng )

\(\Rightarrow\widehat{BAI}=\widehat{CAI}\) (  \(I\in AM\) )

Xét \(\Delta ABI\) và \(\Delta ACI\) có :

AB = AC ( cmt )

\(\widehat{BAI}=\widehat{CAI}\left(cmt\right)\)

Cạnh AI chung 

\(\Rightarrow\Delta BAI=\Delta CAI\left(c-g-c\right)\)

\(\Rightarrow\) IB = IC ( 2 cạnh tương ứng )

 \(\widehat{AIB}=\widehat{AIC}\) ( 2 góc tương ứng )

Có \(\widehat{AIB}=\widehat{AIC}\left(cmt\right)\)

Mà \(\widehat{AIB}+\widehat{AIC}=180^0\) (2 góc kề bù )

\(\Rightarrow2\widehat{AIB}=180^0\)

\(\Rightarrow\widehat{AIB}=90^0\)

Có \(\widehat{AIB}=90^0\left(cmt\right)\)

\(\Rightarrow AI\perp BC\)

Mà \(I\in AM\) ( vẽ thêm )

\(\Rightarrow AM\perp BC\) tại I

Ta có : \(AM\perp BC\) tại M ( cmt )

            IB =IC ( cmt )

\(\Rightarrow\) AM là đường trung trực của BC ( điều phải chứng minh )

Ta có:

 Tam giác ABC cân tại A => góc ABC = góc ACB

Mà góc ABD = góc ACD (=90độ) => góc ABD - góc ABC = góc ACD - góc ACB <=> góc DBC = góc DCB

=> Tam giác DBC cân ở D => DB=DC

b. gỌI I là giao điểm của AD và BC

Ta có: tam giác ABD = tam giác ACD (c-c-c) 

=> góc BAD = góc CAD <=> góc BAI = góc CAI 

=> tam giác BAI = tam giác CAI (c-g-c) => BI=IC

=> AI là trung trực của BC
CMTT có: DI là trung trực BC

=> Đường thẳng AD là trung trực của BC

a: Ta có: NM là đường trung trực của BC

nên NM⊥BC tại M

mà NM⊥AD

nên BC//AD

Ta có: N là điểm nằm trên đường trung trực của BC

nên NB=NC

Xét ΔAND và ΔCNB có 

\(\widehat{AND}=\widehat{CNB}\)

\(\widehat{ADN}=\widehat{CBN}\)

Do đó: ΔAND\(\sim\)ΔCNB

Suy ra: \(\dfrac{AN}{CN}=\dfrac{ND}{NB}\)

\(\Leftrightarrow AN=ND\)

Xét ΔAND có AN=ND

nên ΔNAD cân tại N

b: Ta có: NA+NC=AC

ND+NB=DB

mà NA=ND

và NC=NB

nên AC=DB

Xét tứ giác ABCD có AD//BC

nên ABCD là hình thang

mà AC=DB

nên ABCD là hình thang cân