Bài 9:

\(\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{-3}=\dfrac{z}{-17}=\dfrac{t}{9}=-2\)

=>x=-10; y=6; z=34; t=-18

Bài 10:

\(\Leftrightarrow\dfrac{8}{x}=\dfrac{y}{21}=\dfrac{40}{z}=\dfrac{16}{t}=\dfrac{u}{111}=\dfrac{4}{3}\)

=>x=6; y=28; z=30; t=12; u=148

7B

8D

9D

10C

7:

AM là phân giác

=>BM/AB=CM/AC

=>BM/2=CM/3=(BM+CM)/(2+3)=8/5=1,6

=>BM=3,2cm; CM=4,8cm

5:

a: 2x+6=0

=>x+3=0

=>x=-3

b: (2x-4)(x+3)=0

=>2x-4=0 hoặc x+3=0

=>x=2 hoặc x=-3

c: 5x-7=0
=>5x=7

=>x=7/5

d: 2x(x-3)=0

=>x(x-3)=0

=>x=0 hoặc x-3=0

=>x=0 hoặc x=3

f: =>2x+4+3x-6=5x-1

=>-2=-1(vô lý)

=>PTVN

e: =>5(3x-3)+4(2x-5)=4*5*4=80

=>15x-15+8x-20=80

=>23x=115

=>x=5

Câu 2: 

Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)

a=1; b=-2m-2; \(c=m^2+4\)

\(\text{Δ}=b^2-4ac\)

\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)

\(=4m^2+8m+4-4m^2-16\)

=8m-12

Để phương trình có hai nghiệm phân biệt thì Δ>0

\(\Leftrightarrow8m>12\)

hay \(m>\dfrac{3}{2}\)

Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)

Vì x1 là nghiệm của phương trình nên ta có: 

\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)

\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)

Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)

\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)

\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)

\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)

\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)

\(\Leftrightarrow m^2+8m-20=0\)

Đến đây bạn tự tìm m là xong rồi

Cảm ơn b nha

\(a,\dfrac{1}{3}+\dfrac{1}{5}=\dfrac{5}{15}+\dfrac{3}{15}=\dfrac{8}{15}\)

\(b,\dfrac{11}{8}-\dfrac{3}{4}=\dfrac{11}{8}-\dfrac{6}{8}=\dfrac{5}{8}\)

\(c,6\dfrac{1}{5}x\dfrac{5}{31}=\dfrac{31}{5}x\dfrac{5}{31}=1\)

hình như c hay sao í

a: ĐKXĐ: x<>0; x<>1(A)

(B): x<>0; x<>3

(C): x<>2; x<>-2

b: \(A=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)

\(B=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)

\(C=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)

c: Khi x=0 thì A và B không xác định

Khi x=0 thì C=3/2

Khi x=3 thì B ko xác định, A=2/3; C=3/5

\(a,DKXD:\)

\(+x^2-x\ne0\Leftrightarrow x\ne0;1\)

\(+x^2-3x\ne0\Leftrightarrow x\ne0;3\)

+\(x^2-4\ne0\Leftrightarrow x\ne\pm4\)

\(b,\)

\(\dfrac{2x-2}{x^2-x}=\dfrac{2\left(x-1\right)}{x\left(x-1\right)}=\dfrac{2}{x}\)

\(\dfrac{2x-6}{x^2-3x}=\dfrac{2\left(x-3\right)}{x\left(x-3\right)}=\dfrac{2}{x}\)

\(\dfrac{3x-6}{x^2-4}=\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3}{x+2}\)

\(c,\)

Vì phân thức 1,2 cùng kết quả nên mk lm 1 cái thôi nhé

+ Thay \(x=0\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{0}=0\)

   Thay \(x=3\) vào \(\dfrac{2}{x}\Leftrightarrow\dfrac{2}{3}\) 

+ Thay \(x=0\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{0+2}=\dfrac{3}{2}\)

   Thay \(x=3\) vào \(\dfrac{3}{x+2}\Leftrightarrow\dfrac{3}{3+2}=\dfrac{3}{5}\)

Có phải đề thi ko?

???

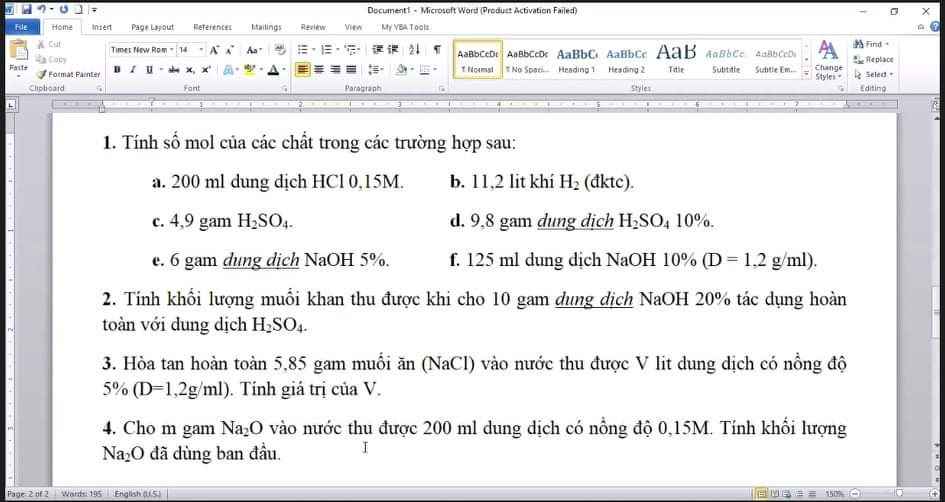
1.

a.\(n_{HCl}=0,2.0,15=0,03\left(mol\right)\)

b.\(n_{H_2}=\dfrac{11,2}{22,4}=0,5\left(mol\right)\)
c.\(n_{H_2SO_4}=\dfrac{4,9}{98}=0,05\left(mol\right)\)

d.\(m_{H_2SO_4}=10\%.9,8=0,98\left(g\right)\Rightarrow n_{H_2SO_4}=\dfrac{0,98}{98}=0,01\left(mol\right)\)

e.\(m_{NaOH}=6.5\%=0,3\left(g\right)\Rightarrow n_{NaOH}=\dfrac{0,3}{40}=0,0075\left(mol\right)\)

f.\(m_{ddNaOH}=125.1,2=150\left(g\right)\Rightarrow m_{NaOH}=150.20\%=30\left(g\right)\)

\(\Rightarrow n_{NaOH}=\dfrac{30}{40}=0,75\left(mol\right)\)

2.

\(m_{NaOH}=10.20\%=2\left(g\right)\Rightarrow n_{NaOH}=\dfrac{2}{40}=0,05\left(mol\right)\)

PTHH: 2NaOH + H₂SO₄ → Na₂SO₄ + H₂O

Mol:      0,05                           0,025

\(\Rightarrow m_{Na_2SO_4}=0,025.142=3,55\left(g\right)\)

3.

\(n_{NaCl}=\dfrac{5,85}{58,5}=0,1\left(mol\right)\)

PTHH: 2NaCl + 2H₂O → 2NaOH + Cl₂ + H₂

Mol:      0,1                         0,1

\(m_{NaOH}=0,1.40=4\left(g\right)\Rightarrow m_{ddNaOH}=\dfrac{4.100\%}{5\%}=80\left(g\right)\)

\(\Rightarrow V_{ddNaOH}=\dfrac{80}{1,2}=66,7\left(ml\right)\)