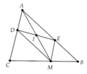
Cho \(\bigtriangleup\text{ABC}\), điểm M nằm trên cạnh BC. Qua M dựng đường thẳng song song với AB cắt AC tại D, qua M dựng đường thẳng song song với AC cắt AB tại E.
a/ Chứng minh \(\diamond\text{ADME}\) là tứ giác gì, vì sao ?
b/ Tìm vị trí của điểm M trên cạnh AB để \(\diamond\text{ADME}\) là hình thoi.
c/ Tìm điều kiện của điểm M trên cạnh AB để \(\diamond\text{ADME}\) là hình chữ nhật.



\(\text{GIẢI :}\)
a) Xét \(\diamond\text{ADME}\) có \(DM\text{ }//\text{ }AB\), \(EM\text{ }//\text{ }AC\) \(\Rightarrow\text{ }\diamond\text{ADME}\) là hình bình hành.
b) Để hình bình hành ADME là hình thoi \(\Leftrightarrow\text{ }AM\) là tia phân giác của góc A.
Vậy M là giao điểm của tia phân giác góc A và cạnh BC thì ADME là hình thoi.
c) Để hình bình hành ADME là hình chữ nhật \(\Leftrightarrow\angle\text{A}=90^0\text{ }\Leftrightarrow\text{ }\bigtriangleup\text{ABC}\) vuông tại A.