cho tam giác ABC vuông tại A
quaC kẻ đường thăng d vuông góc với Ac
Trên d lấy điểm E sao cho CE=AB(EvàB thuộc 2 nửa mp đối nhau bờ AC)
a) C/m BC//AE và BC=AE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 3 2022
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
Suy ra: BC//AE và BC=AE
17 tháng 12 2023
a: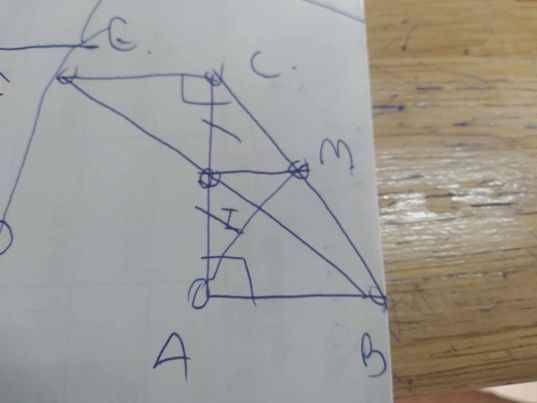 
b:
Ta có: CE\(\perp\)CA
AB\(\perp\)CA
Do đó: CE//AB
Xét ΔCEB và ΔABE có
CE=AB
\(\widehat{CEB}=\widehat{ABE}\)(hai góc so le trong, AB//CE)
BE chung
Do đó: ΔCEB=ΔABE
=>CB=AE
Ta có: ΔCEB=ΔABE
=>\(\widehat{CBE}=\widehat{AEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên CB//AE
c: MI//CE
CE//AB
Do đó: MI//AB
Ta có: MI//AB
AB\(\perp\)AC
Do đó: MI\(\perp\)AC
Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
Ta có: ΔMAC cân tại M
mà MI là đường cao
nên MI là phân giác của \(\widehat{AMC}\)
d: Ta có: \(\widehat{MAC}+\widehat{MAB}=\widehat{BAC}=90^0\)
\(\widehat{MCA}+\widehat{MBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{MAC}=\widehat{MCA}\)(ΔAMC cân tại M)
nên \(\widehat{MAB}=\widehat{MBA}\)
=>ΔMAB cân tại M
Xét ΔMAB cân tại M có \(\widehat{MBA}=60^0\)
nên ΔMAB đều
=>\(\widehat{BAM}=60^0\)
e: Xét ΔECI vuông tại C và ΔBAI vuông tại A có
EC=BA
CI=AI
Do đó:ΔECI=ΔBAI
=>\(\widehat{EIC}=\widehat{BIA}\)
mà \(\widehat{EIC}+\widehat{EIA}=180^0\)(hai góc kề bù)
nên \(\widehat{EIA}+\widehat{BIA}=180^0\)
=>B,I,E thẳng hàng