Tính chiều cao của cây trong hình bên dưới (làm tròn đến mét)?
A.21m
B.20m
C.17m
D.22m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kí hiệu như hình vẽ.
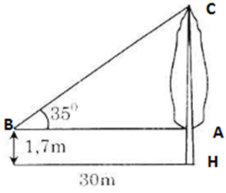
Trong tam giác vuông ABC có:
BA = AC.tan35o = 30.tan35o ≈ 21 (m)
Chiều cao của cây là:
BH = BA + AH ≈ 21 + 1,7 ≈ 22,7 (m)
Vậy chiều cao của cây là 22,7 (m) (hoặc = 227 dm).
(Ghi chú: Bạn cũng có thể làm tắt hơn như sau:
Chiều cao của cây là:
BH = BA + AH = AC.tan35o + AH = 30.tan35o + 1,7 = 22,7 m)

Kí hiệu như hình vẽ.
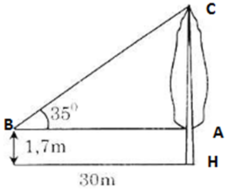
Trong tam giác vuông ABC có:
B A = A C . tan 35 ° = 30 . tan 35 ° ≈ 21 ( m )
Chiều cao của cây là:
BH = BA + AH ≈ 21 + 1,7 ≈ 22,7 (m)
Vậy chiều cao của cây là 22,7 (m) (hoặc = 227 dm).
(Ghi chú: Bạn cũng có thể làm tắt hơn như sau:
Chiều cao của cây là:
B H = B A + A H = A C . tan 35 ° + A H = 30 . tan 35 ° + 1 , 7 = 22 , 7 m )

Chiều cao của cây là: h = 1,7 + 20. tan 35 0 ≈ 15,7m
Đáp án cần chọn là: B

Bài 2
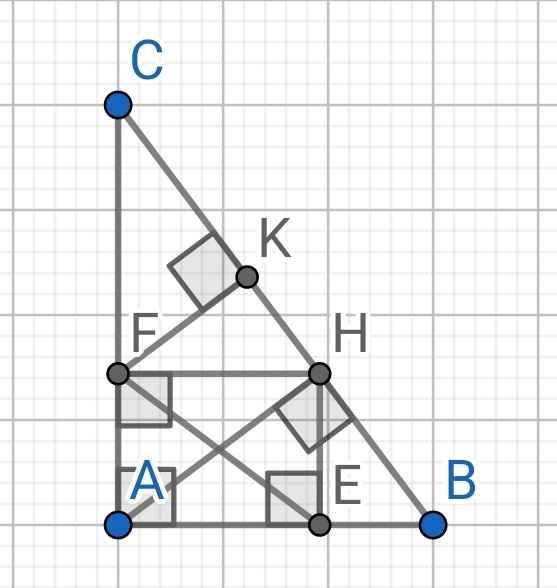 a) ∆ABC vuông tại A, AH là đường cao
a) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.HC
= 4.9
= 36
⇒ AH = 6 (cm)
BC = BH + HC
= 4 + 9 = 13 (cm)
∆ABC vuông tại A, AH là đường cao
⇒ AB² = BH.BC
= 4.13
= 52 (cm)
⇒ AB = 2√13 (cm)
⇒ cos ABC = AB/BC
= 2√13/13
⇒ ∠ABC ≈ 56⁰
b) ∆AHB vuông tại H, HE là đường cao
⇒ AH² = AE.AB (1)
∆AHC vuông tại H, HF là đường cao
⇒ AH² = AF.AC (2)
Từ (1) và (2) suy ra:
AE.AB + AF.AC = 2AH² (3)
Xét tứ giác AEHF có:
∠HFA = ∠FAE = ∠AEH = 90⁰ (gt)
⇒ AEHF là hình chữ nhật
⇒ AH = EF (4)
Từ (3) và (4) suy ra:
AE.AB + AF.AC = 2EF²
Bài 1
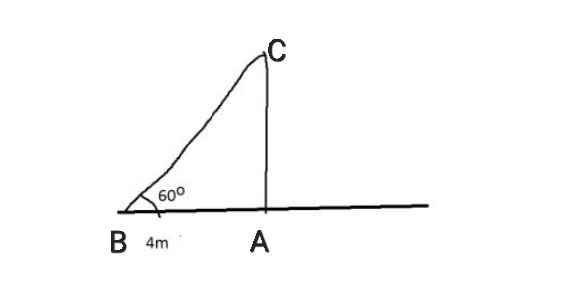 Ta có:
Ta có:
tan B = AC/AB
⇒ AC = AB . tan B
= 4 . tan60⁰
= 4√3 (m)
≈ 7 (m)

Chiều cao của cây:
\(h=20.tan30^0\approx12\left(m\right)\)

Sửa đề: Chiều dài từ gốc cây đến chỗ cây bị gãy là 3m
Gọi A là gốc của cái cây
Gọi Clà ngọn của cái cây
Gọi B là chỗ cây bị gãy
Do đó, ta có: \(AB\perp AC\)
Theo đề, ta có: BC=7m; AB=3m
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{7^2-3^2}=2\sqrt{10}\left(m\right)\simeq6,3\left(m\right)\)

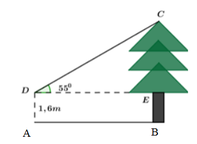
Đặt các điểm D, E như hình vẽ.
Xét CDE vuông tại E ta có:
![]()
Chiều cao của cây là BC = CE + BE = 8,57 + 1,6 = 10,17m
Đáp án cần chọn là: D
Trong tam giác vuông ABC:
\(AC=BC.tan40^0=24.tan40^0\)
\(\Rightarrow AD=AC+CD=24.tan40^0+1,6\approx22\left(m\right)\)