cho 3 điểm A (0;1), B (12;5), C (-3;5). Tìm phương trình đường thẳng cách đều ba điểm A, B, C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các điểm nằm trên trục hoành là các điểm có tung độ bằng 0. Trong số các điểm ở trên ta thấy những điểm có tung độ bằng 0 là: A(-1; 0), D(3; 0), O(0; 0) . Vậy có ba điểm nằm trên trục hoành
Chọn đáp án D

Thay tọa độ A vào (d) thỏa mãn \(\Rightarrow A\in d\Rightarrow d\left(A;d\right)=0\)
\(\Rightarrow d\left(K;d\right)=0\Rightarrow K\in d\)
\(\Rightarrow K\) là giao điểm của d và trục Ox
Tọa độ K là nghiệm: \(\left\{{}\begin{matrix}y=0\\2x-y-3=0\end{matrix}\right.\)
\(\Rightarrow K\left(\dfrac{3}{2};0\right)\)

Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.

Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.

Gọi d: y = ax + b là đường thẳng đi qua A và B
A ( 0 ; 3 ) ∈ ( d ) ⇔ a . 0 + b = 3 ⇔ b = 3 B ( 2 ; 2 ) ∈ ( d ) ⇔ a . 2 + b = 2 ⇒ b = 3 2 a + b = 2 ⇔ b = 3 a = − 1 2 ⇒ d : y = − 1 2 x + 3
Để 2 điểm A, B, C thẳng hàng thì C ( m + 3 ; m ) ∈ ( d ) y = − 1 2 x + 3
⇔ m = − 1 2 ( m + 3 ) + 3 ⇔ 3 2 m = 3 2 ⇒ m = 1
Vậy m = 1
Đáp án cần chọn là: A

a) gọi đường thẳng đi qua \(A;B\) có dạng : \(\left(d\right):y=cx+d\)
vì \(A;B\in\left(d\right)\) \(\Rightarrow\left\{{}\begin{matrix}ac+d=0\\d=b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}d=b\\c=\dfrac{-d}{a}=\dfrac{b}{a}\end{matrix}\right.\)
\(\Rightarrow\left(d\right):y=\dfrac{b}{a}x+b\)
b) để \(A;B;C\) thẳng hàng \(\Leftrightarrow C\in\left(d\right)\)
\(\Leftrightarrow\dfrac{b}{a}+b=2\Leftrightarrow b\left(\dfrac{1}{a}+1\right)=2\)
c) từ \(b\left(\dfrac{1}{a}+1\right)=2\Leftrightarrow b=\dfrac{2a}{a+1}\)
ta có : \(A\in Ox\) và \(B\in Oy\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}\sqrt{a^2}\sqrt{b^2}=\dfrac{1}{2}ab=\dfrac{1}{2}a\dfrac{2a}{a+1}\)
\(=\dfrac{a^2}{a+1}=S\)
\(\Leftrightarrow a^2-Sa-S=0\) phương trình này luôn có nghiệm \(\Rightarrow\Delta\ge0\)
\(\Leftrightarrow S^2+4S\ge0\Leftrightarrow S\left(S+4\right)\ge0\Leftrightarrow S\ge0\)
dấu "=" xảy ra khi \(a=0\) ; \(b=0\)
saint suppapong udomkaewkanjana ĐP Nhược Giang Nguyễn Thanh Hằng Ngô Kim Tuyền Ngô Thành Chung Mysterious Person Mashiro Shiina Fa Châu De DDTank JakiNatsumi

Ta có: AB → = (−1; −2; 1)
AC → = (−1; −3; 0)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB → và AC → cùng phương, nghĩa là AB → = k AC → với k là một số thực.
Giả sử ta có AB → = k AC →
khi đó 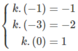
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.

Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\mx-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{m}\\y=0\end{matrix}\right.\)
=>B(3/m;0)
\(OB=\sqrt{\left(\dfrac{3}{m}-0\right)^2+\left(0-0\right)^2}=\sqrt{\dfrac{9}{m^2}}=\dfrac{3}{\left|m\right|}\)
\(OA=\sqrt{\left(0-0\right)^2+\left(-3-0\right)^2}=3\)
OA=2OB
=>\(3=\dfrac{6}{\left|m\right|}\)
=>|m|=6/3=2
=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)
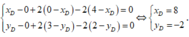
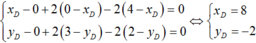
Bạn viết pt 3 đường trung bình của tam giác ABC ra là được thôi
Vì A, B, C không nằm trên cùng một đường thằng, nên đường thẳng cách đều 3 điểm A. B, C là 3 đường trung bình của tam giác ABC
Gọi D, E, F lần lượt là trung điểm của AB, BC và CA, ta có: \(D\left(6;3\right)\); \(E\left(\frac{9}{2};5\right)\); \(F\left(-\frac{3}{2};3\right)\)
Gọi \(d_1,d_2,d_3\) là 3 đường thằng cần tìm. VTCP của \(\overrightarrow{u_{d_1}};\overrightarrow{u_{d_2}};\overrightarrow{u_{d_3}}\) lần lượt là \(\overrightarrow{BC};\overrightarrow{CA};\overrightarrow{AB}\)
\(d_1:\left\{{}\begin{matrix}QuaD\\VTCP\overrightarrow{u_1}\end{matrix}\right.\)
\(d_2:\left\{{}\begin{matrix}QuaE\\VTCP\overrightarrow{u_2}\end{matrix}\right.\)
\(d_3:\left\{{}\begin{matrix}QuaF\\VTPT\overrightarrow{u_3}\end{matrix}\right.\)
Viết các phương trình tham số, kết luận.