cầu được giúp đỡ câu D
Tam giác ABC nội tiếp trong đường tròn O có AC > AB. Gọi D là điểm chính giữa của cung nhỏ BC, P là giao điểm của AB và CD. Tiếp tuyến của đường tròn tại C cắt tiếp tuyến của đường tròn tại D tại E và cắt AD tại Q
a) Chứng minh DE //BC
b) chứng minh tam giác PACQ nội tiếp
c) chứng minh DE //PQ
d) chứng minh nếu F là giao điểm của AD và BC thì
\(\frac{1}{CE}=\frac{1}{CQ}+\frac{1}{CF}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chứng minh tứ giác OBDK nội tiếp:
dựa vào góc DBK=DOK (vì hai góc cùng chắn cung DK)
vậy, ta cần chứng minh DBK=DOK
đặt giao của OM với AB là H
dễ dàng chứng minh: DBK=BOA=1/2 BOC (1)
có M thuộc (O) và tiếp tuyến CD của M nên chứng minh được tam giác OBD=OMD (ch,cgv)
=> góc BOD=DOM và MOE=COE (chứng minh tương tự)
=> DOM+EOM=DOE=1/2BOM+1/2MOC=1/2BOC (2)
từ (1),(2) => DOK=KBD (đpcm)

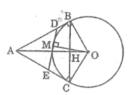
Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:
A O 2 = A B 2 + B O 2
Suy ra: A B 2 = A O 2 - B O 2 = 5 2 - 3 2 = 16
AB = 4 (cm)
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB = 2.4 = 8 (cm)