Cho tui tick nha

Diện tích tam giác ABN = 1/4 diện tích tam giác ABC vì có chung chiều cao nối từ A xuống N và BN = 1/4 BC 

Diện tích tam giác ABN là: 

64 x 1/4 = 16 (cm2 ) 

Diện tích tam giác BMN = 1/2 diện tích tam giác ABN vì có chung chiều cao nối từ N xuống M và BM = 1/2 BA 

Diện tích tam giác BMN là: 

16 x 1/2 = 8 (cm2 ) 

Đáp số: 8 cm2 

8 cm vuông

đs: 35

đùa thôi,ko phải 35

\(\dfrac{CP}{CA}=\dfrac{2}{3}\Rightarrow\dfrac{AP}{CA}=\dfrac{1}{3}\)

Hai tg ABP và tg ABC có chung đường cao từ B->CA nên

\(\dfrac{S_{ABP}}{S_{ABC}}=\dfrac{AP}{CA}=\dfrac{1}{3}\Rightarrow S_{ABP}=\dfrac{1}{3}xS_{ABC}\)

Hai tg AMP và tg ABP có chung đường cao từ P->AB nên

\(\dfrac{S_{AMP}}{S_{ABP}}=\dfrac{AM}{AM}=\dfrac{1}{4}\Rightarrow S_{AMP}=\dfrac{1}{4}xS_{ABP}=\dfrac{1}{4}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{12}xS_{ABC}\)

\(S_{BCP}=S_{ABC}-S_{ABP}=S_{ABC}-\dfrac{1}{3}xS_{ABC}=\dfrac{2}{3}xS_{ABC}\)

\(\dfrac{BN}{BC}=\dfrac{2}{3}\Rightarrow\dfrac{CN}{BC}=\dfrac{1}{3}\)

Hai tg CNP và tg BCP có chung đường cao từ P->BC nên

\(\dfrac{S_{CNP}}{S_{BCP}}=\dfrac{CN}{BC}=\dfrac{1}{3}\Rightarrow S_{CNP}=\dfrac{1}{3}xS_{BCP}=\dfrac{1}{3}x\dfrac{2}{3}xS_{ABC}=\dfrac{2}{9}xS_{ABC}\)

\(\dfrac{AM}{AB}=\dfrac{1}{4}\Rightarrow\dfrac{BM}{AB}=\dfrac{3}{4}\)

Hai tg BCM và tg ABC có chung đường cao từ C->AB nên

\(\dfrac{S_{BCM}}{S_{ABC}}=\dfrac{BM}{AB}=\dfrac{3}{4}\Rightarrow S_{BCM}=\dfrac{3}{4}xS_{ABC}\)

Hai tg BMN và tg BCM có chung đường cao từ M->BC nên

\(\dfrac{S_{BMN}}{S_{BCM}}=\dfrac{BN}{BC}=\dfrac{2}{3}\Rightarrow S_{BMN}=\dfrac{2}{3}xS_{BCM}=\dfrac{2}{3}x\dfrac{3}{4}xS_{ABC}=\dfrac{1}{2}xS_{ABC}\)

\(S_{MNP}=S_{ABC}-S_{AMP}-S_{CNP}-S_{BMN}=\)

\(=S_{ABC}-\dfrac{1}{12}xS_{ABC}-\dfrac{2}{9}xS_{ABC}-\dfrac{1}{2}xS_{ABC}=\)

\(=\dfrac{11}{36}xS_{ABC}\)

cô làm rồi em nhé

https://olm.vn/cau-hoi/cho-tam-giac-abc-co-dien-tich-180-cm2-tren-cac-canh-ab-bc-ca-lan-luot-lay-cac-diem-m-n-p-sao-cho-am-23-ab-bn-34-bc-va-cp-13-ca-tinh-di.8088189515587

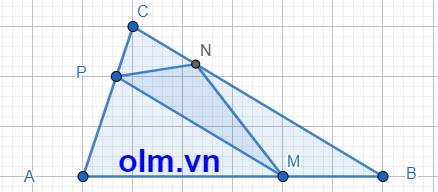
AP = AC - PC = AC - \(\dfrac{1}{3}\)AC = \(\dfrac{2}{3}\)AC

S_AMP = \(\dfrac{2}{3}\)S_ACM  (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AC và AP = \(\dfrac{2}{3}\)AC)

S_ACM = \(\dfrac{2}{3}\)S_ABC (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và AM = \(\dfrac{2}{3}\)AB)

S_AMP = \(\dfrac{2}{3}\times\dfrac{2}{3}\)S_ABC = 180 \(\times\dfrac{4}{9}\) = 80 (cm²)

S_BMN = \(\dfrac{3}{4}\)S_BCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC  và BN = \(\dfrac{3}{4}\)BC)

BM = AB - AM = AB - \(\dfrac{2}{3}\)AB = \(\dfrac{1}{3}\)AB

S_BCM = \(\dfrac{1}{3}\)S_ABC( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{1}{3}\)AB)

S_BMN = \(\dfrac{3}{4}\times\dfrac{1}{3}\)S_ABC = 180 \(\times\dfrac{1}{4}\)  = 45 (cm²)

CN = BC - BN = BC - \(\dfrac{3}{4}\)BC  = \(\dfrac{1}{4}\)BC 

S_CPN = \(\dfrac{1}{4}\)S_CPB ( vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{4}\)BC)

S_CBP = \(\dfrac{1}{3}\)S_ABC  ( vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và CP = \(\dfrac{1}{3}\)CA)

S_CPN = \(\dfrac{1}{4}\times\dfrac{1}{3}\)S_ABC = 180 \(\times\) \(\dfrac{1}{12}\) = 15 (cm²)

Diện tích tam giác MNPQ là:

180 - ( 80 + 45 + 15) = 40 (cm²)

Đáp số 40 cm²

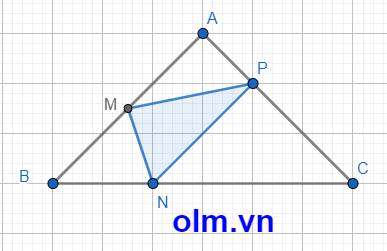
S_AMP = \(\dfrac{1}{2}\)S_ABP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AB và AM = \(\dfrac{1}{2}\)AB)

AP = AC - PC = AC - \(\dfrac{2}{3}\) AC = \(\dfrac{1}{3}\)AC

S_APB = \(\dfrac{1}{3}\)S_ABC (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và AP = \(\dfrac{1}{3}\) AC)

⇒ S_AMP  = \(\dfrac{1}{2}\times\)\(\dfrac{1}{3}\)S_ABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm²)

S_BMN = \(\dfrac{1}{2}\)S_ABN (vì hai tam giác có chung chiều cao hạ từ đỉnh N xuống đáy AB  và BM = \(\dfrac{1}{2}\) AB)

S_ABN = \(\dfrac{1}{3}\)S_ABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BN = \(\dfrac{1}{3}\)BC)

S_BMN = \(\dfrac{1}{2}\times\) \(\dfrac{1}{3}\)S_ABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm²)

CN = BC - BN =  BC - \(\dfrac{1}{3}\)BC = \(\dfrac{2}{3}\)BC

S_CNP = \(\dfrac{2}{3}\)S_BCP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{2}{3}\) BC)

S_BCP = \(\dfrac{2}{3}\)S_ABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và PC = \(\dfrac{2}{3}\)CA)

S_CNP = \(\dfrac{2}{3}\times\dfrac{2}{3}\) = \(\dfrac{4}{9}\)\(\times\)36 = 16 (cm²)

Diện tích tam giác MNP là:

36 - (6+6+16) = 8 (cm²)

Đáp số: 8 cm²