cho tam giác ABC nột tiếp (O). phân giác gsc A cắt (O) tại I. CI cắt AB tại M. Tiếp tuyến tại C cắt AI tại N.CM góc BMI = GÓC INC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi giao điểm của hai tia MA và BI là J.
Ta thấy I là tâm nội tiếp \(\Delta\)ABC, CI cắt (ABC) tại M. Suy ra M là điểm chính giữa cung AB không chứa C.
Từ đó ta có biến đổi góc ^AJB = 1800 - ^AMB - ^IBM = (^ACB - ^ABC)/2 = ^AKB
Suy ra tứ giác ABKJ nội tiếp. Mà BJ là phân giác góc ABK nên (JA = (JK hay JA = JK
Đồng thời IM // JK (Vì ^JKB = ^BAM = ^BCM)
Mặt khác ^MAI = ^MIA = (^BAC + ^ACB)/2 nên MI = MA. Áp dụng ĐL Thales ta có:
\(\frac{MI}{KJ}=\frac{AM}{AJ}=\frac{NI}{NJ}\). Kết hợp với ^MIN = ^KJN (IM // JK) suy ra \(\Delta\)MIN ~ \(\Delta\)KJN (c.g.c)
Suy ra ^MNI = ^KNJ. Lại có I,N,J thẳng hàng, dẫn đến M,N,K thẳng hàng (đpcm).

a: góc BEH+góc BKH=180 độ
=>BEHK nội tiếp
=>góc EBH=góc EKH
góc BKA=góc BDA=90 độ
=>ABKD nội tiếp
=>góc EBH=góc AKD=góc EKH
=>KA là phân giác của góc EKD
b: góc AIO=góc AJO=góc AKO=90 độ
=>I,J,K,A,O cùng thuộc đường tròn đường kính OA
sđ cung AI=sđ cung AJ
=>góc AKI=góc AJI
=>góc AKE+góc IKE=góc AKD+góc DKJ
=>góc IKE=góc DKJ
c:

a: Xét tứ giác OBDC có \(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
nên OBDC là tứ giác nội tiếp
=>\(\widehat{DOC}=\widehat{DBC}\left(1\right)\)
Xét (O) có
\(\widehat{DBC}\) là góc tạo bởi tiếp tuyến BD và dây cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{DBC}=\widehat{BAC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{DOC}=\widehat{BAC}\)
b: Ta có: DI//AB
=>\(\widehat{CID}=\widehat{CAB}\)(hai góc đồng vị)
mà \(\widehat{CAB}=\widehat{DBC}\)
và \(\widehat{DBC}=\widehat{DOC}\)
nên \(\widehat{CID}=\widehat{COD}\)
=>CIOD là tứ giác nội tiếp
c: ta có: CIOD là tứ giác nội tiếp
=>\(\widehat{OID}=\widehat{OCD}=90^0\)
=>OI\(\perp\)EF tại I
Ta có: ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
=>IE=IF

Lời giải:
a. Ta thấy $\widehat{AHC}=90^0$ (góc nt chắn nửa đường tròn $(O)$ - chắn đường kính AC)
$\Rightarrow AH\perp HC$ hay $AH\perp BC$ (đpcm)
b. Do tam giác $BHA$ vuông tại $H$ nên đường trung tuyến $HM$ bằng nửa cạnh huyền $BA$
$\Rightarrow HM=MA$
$\Rightarrow \widehat{MHA}=\widehat{MAH}=\widehat{BAH}=90^0-\widehat{HAC}=\widehat{HCA}$
$\Rightarrow HM$ là tiếp tuyến $(O)$.
c.
Dễ thấy $\widehat{ADC}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow DA\perp DC$
$\Rightarrow \frac{DA}{DC}=\cot \widehat{DAC}=\cot A_1(*)$
$\frac{DC}{DE}=\cot \widehat{DCE}=\cot C_1$
Mà $\widehat{C_1}=90^0-\widehat{E_1}=90^0-\widehat{E_2}=\widehat{A_2}=\widehat{A_1}$
$\Rightarrow \frac{DC}{DE}=\cot C_1=\cot A_1(**)$
Từ $(*); (**)\Rightarrow \frac{DA}{DC}=\frac{DC}{DE}\Rightarrow DA.DE=DC^2$
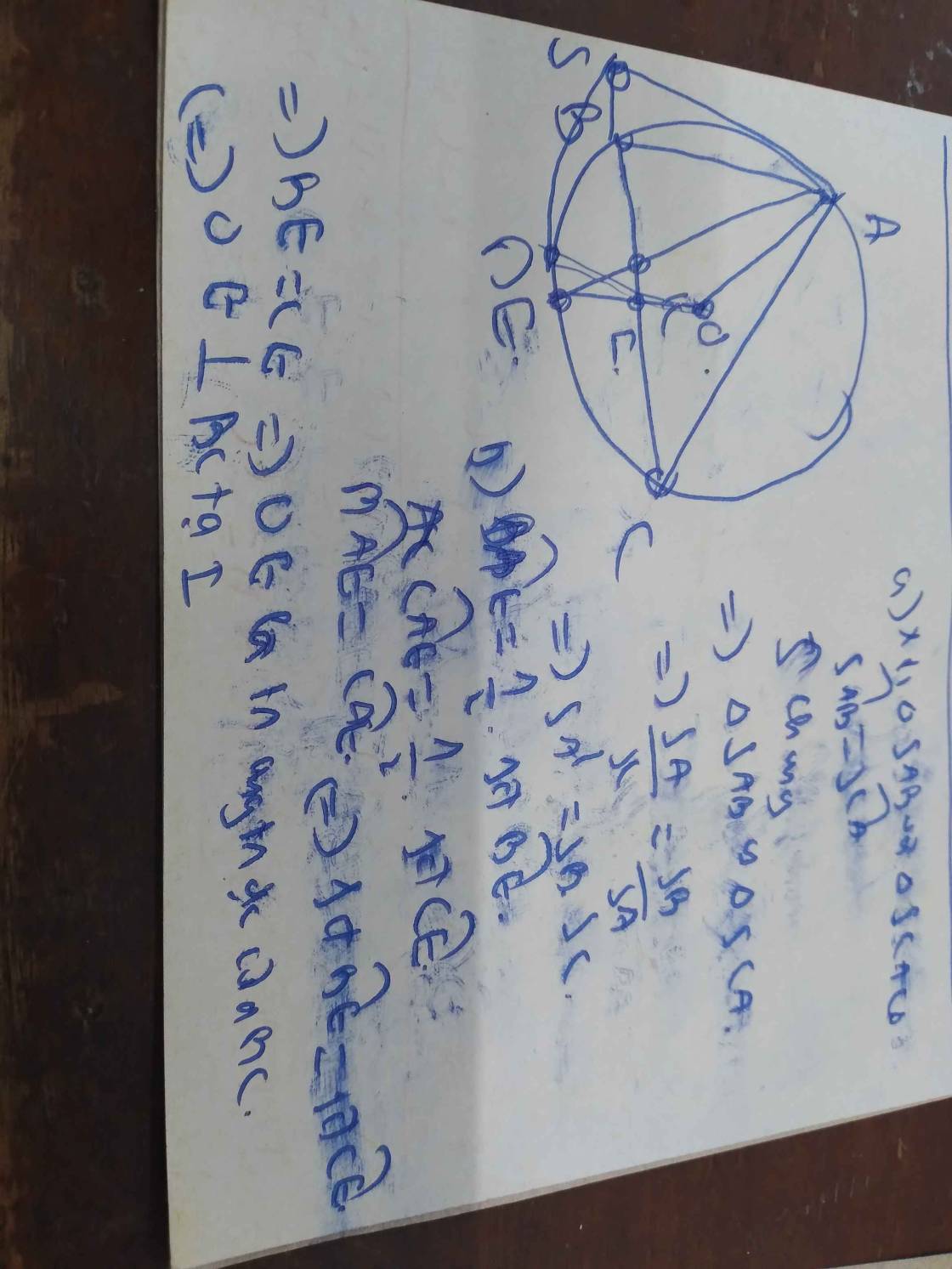
Ta có:
\(\widehat{ICN}=\widehat{IAC}\) (hệ quả góc tạo bởi t.tuyến và dây cung)
\(\widehat{AIM}=\widehat{CIN}\) (đối đỉnh)
\(\Rightarrow\Delta AIM~\Delta CIN\left(g-g\right)\Rightarrow\widehat{BIM}=\widehat{INC}\)