b: 4x^2-20x+25=(x-3)^2

=>(2x-5)^2=(x-3)^2

=>(2x-5)^2-(x-3)^2=0

=>(2x-5-x+3)(2x-5+x-3)=0

=>(3x-8)(x-2)=0

=>x=8/3 hoặc x=2

c: x+x^2-x^3-x^4=0

=>x(x+1)-x^3(x+1)=0

=>(x+1)(x-x^3)=0

=>(x^3-x)(x+1)=0

=>x(x-1)(x+1)^2=0

=>\(x\in\left\{0;1;-1\right\}\)

d: 2x^3+3x^2+2x+3=0

=>x^2(2x+3)+(2x+3)=0

=>(2x+3)(x^2+1)=0

=>2x+3=0

=>x=-3/2

a: =>x^2(5x-7)-3(5x-7)=0

=>(5x-7)(x^2-3)=0

=>\(x\in\left\{\dfrac{7}{5};\sqrt{3};-\sqrt{3}\right\}\)

cho mik hỏi rằng là 3x2 + 4x = 0 hay  3x² + 4x = 0

 3x² + 4x = 0

\(\Leftrightarrow x\left(x^2-7x-8\right)=0\\ \Leftrightarrow x\left(x^2-8x+x-8\right)=0\\ \Leftrightarrow x\left(x-8\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=8\\x=-1\end{matrix}\right.\)

x₁=1

x₂=\(\dfrac{-2}{7}\)

\(21x^3-15x^2-6x=0\\ \Leftrightarrow x\left(21x^2-15x-6\right)=0\\ \Leftrightarrow x\left[\left(21x^2-21x\right)+\left(6x-6\right)\right]=0\\ \Leftrightarrow x\left[21x\left(x-1\right)+6\left(x-1\right)\right]=0\\ \Leftrightarrow x\left(x-1\right)\left(21x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{-2}{7}\end{matrix}\right.\)

​​​​​​​​​​giải phương trình (x3+7x2+6x-30)/(x3-1)=(x2-x+16)/(x2+x+1)

có dấu nào là dấu nhân ko hay toàn là x hết

Ta có:  2 x 2 + 3 2  -10 x 3  -15x =0 ⇔  2 x 2 + 3 2  - 5x(2 x 2  +3)=0

⇔ (2 x 2 +3)( 2 x 2  +3 - 5x) = 0 ⇔ (2 x 2  +3)( 2 x 2  - 5x +3)=0

Vì 2 x 2   ≥ 0 nên 2 x 2  +3 > 0

Suy ra : 2x2 - 5x +3=0

∆ =  - 5 2 -4.2.3 =25 -24=1 > 0

∆ = 1  = 1

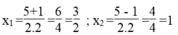
vậy phương trình đã cho có 2 nghiệm: x1 = 3/2 ; x2 = 1

Điều kiện : x ≠ 1

Ta có:

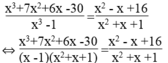
⇔  x 3 +7 x 2  +6x -30 = ( x 2  –x +16)(x -1)

⇔  x 3 +7 x 2  +6x -30 =  x 3  –  x 2  –  x 2  +x +16x -16

⇔ 9 x 2  -11x -14 =0

∆  = - 11 2  -4.9.(-14) = 121 +504 = 625 > 0

∆ ' = 625  =25

Giá trị của x thỏa mãn điều kiện bài toán

Vậy nghiệm của phương trình là x = -7/9 và x = 2