a)phương trình cân bằng nhiệt 

\(Q_{thu}=Q_{tỏa}\)

\(=>Q_{thu}=m_1.c_1.\Delta t_1=0,5.380.\left(120-20\right)=19000J\)

b) nước nóng lên thêm số độ là

\(\Delta t^o=\dfrac{Q_{thu}}{m_1.c_1}=\dfrac{19000}{0,5.4200}\approx9,05^oC\)

Ta có phương trình cân bằng nhiệt

\(Q_{thu}=Q_{tỏa}\\ \Leftrightarrow0,5.380\left(120-20\right)=0,5.4200\left(20-t_1\right)\) 

( giải pt )

\(\Rightarrow t_1=10,95238^o\approx11^o\)

Nhiệt lượng nước nhận được bằng đúng nhiệt lượng do miếng đồng tỏa ra là:

Q2 = Q1 = m1.c1.(t1 - t) = 0,5.380.(80 - 20) = 11400 J

Độ tăng nhiệt độ của nước là:

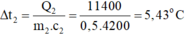
Tóm tắt:

\(m_1=0,5kg\)

\(m_2=500g=0,5kg\)

\(t_1=80^oC\)

\(t=20^oC\)

\(\Rightarrow\Delta t_1=t_1-t=80-20=60^oC\)

\(c_1=380J/kg.K\)

\(c_2=4200J/kg.K\)

===========

\(Q_2=?J\)

\(\Delta t_2=?^oC\)

Do nhiệt lượng của quả cầu tỏa ra bằng nhiệt lượng của nước nhận vào nên:

\(Q_2=Q_1=m_1.c_1.\Delta t_1=0,5.380.60=11400J\)

Nhiệt độ mà nước tăng thêm:

Theo phương trình cân bằng nhiệt:

\(Q_1=Q_2\)

\(\Leftrightarrow11400=m_2.c_2.\Delta t_2\)

\(\Leftrightarrow\Delta t_2=\dfrac{11400}{m_2.c_2}\)

\(\Leftrightarrow\Delta t_2=\dfrac{11400}{0,5.4200}\approx5,4^oC\)

Ta có phương trình cân bằng nhiệt

\(Q_{toả}=Q_{thu}\)

--> Nhiệt lượng nước nhận đc là

\(Q_{thu}=0,5.380\left(100-40\right)=11400J\)

Độ tăng nhiệt của nước

\(\Delta t=\dfrac{Q}{mc}=\dfrac{11400}{0,5.4200}=5,42^o\)

nước nhận được một nhiệt lượng

\(Q_{thu}=Q_{tỏa}=m_1.c_1.\Delta t_1=0,5.380.\left(100-40\right)=11400J\)

nước  nóng thêm

\(\Delta t_1=\dfrac{Q_{thu}}{m_1c_1}=\dfrac{11400}{0,5.4200}=5,43^0C\)

Ta có pt cân bằng nhiệt

\(Q_{thu}=Q_{tỏa}\\ \Rightarrow Q_{thu}=0,5.380\left(80-20\right)=11400J\) 

Nước nóng thêm số độ 

\(\Delta t^o=\dfrac{Q_{thu}}{mc}=\dfrac{11400}{0,5.4200}=5,42^o\)

Ta có : Q1 = m1.c1.(t1 - t) =0.5.380.(80-20) = 11400 
Q2 = m2.c2.(t - t2) = 0,5.4200.(20 - t2) = 42000 - 2100.t2 
Theo pt cân bằng nhiệt , ta có : 
Q1 = Q2 
11400 = 42000 - 2100.t2 
t2 = 14,57 
t' = t - t2 = 20 - 14,57 = 5,43 
Vậy nước nhận một nhiệt lượng là 11400 và nóng lên 5,43 độ 
Chúc bạn học tốt 

Em cảm ơn ạ

Tóm tắt:

\(m_1=0,5kg\\ t_1=80^0C\\ t_2=15^0C\\ t=20^0C\\ \Rightarrow\Delta t_1=t_1-t=80-20=60^0C\\ \Rightarrow\Delta t_2=t-t_2=20-15=5^0C\\ c_1=380J/kg.K\\ c_2=4200J/kg.K\)

____________

\(m_2=?kg\)

Giải

Khối lượng của nước là:

Theo pt cân bằng nhiệt:

\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\\ \Leftrightarrow0,5.380.60=m_2.4200.5\\ \Leftrightarrow11400=21000m_2\\ \Leftrightarrow m_2\approx0,54kg\)

Tóm tắt

`m_1=0,5kg`

`c_1=380J//kg.K`

`t_1=80^o C`

`t_2=15^oC`

`c_2=4200J//kg.K`

`t=20^oC`

`m_2=???kg`

Giải

Nhiệt lượng của miếng đồng tỏa ra là

`Q_1=m_1 c_1 (t_1 -t)=0,5*380*(80-20)=11400(J)`

Nhiệt lượng của nước thu vào là

`Q_2=m_2 c_2 (t-t_2 )=m_2 * 4200(20-15)=21000m_2 (J)`

Áp dụng phương trinh cân bằng nhiệt

`Q_1=Q_2

`<=>11400=21000m_2`

`<=>m_2=0,542(kg)`