Trong không gian với hệ trục tọa độ Oxyz. Cho ba điểm A(1,1,1),B(2,4,6),C(0,2,3). Số đường thẳng cách đều ba điểm đó là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Gọi I là trung điểm của AB suy ra 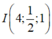 và (P) là mặt phẳng trung trực của đoạn AB.
và (P) là mặt phẳng trung trực của đoạn AB.
Mặt phẳng (P) đi qua I và nhận ![]() làm vec tơ pháp tuyến có phương trình là:
làm vec tơ pháp tuyến có phương trình là:
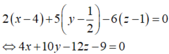
Gọi J là trung điểm của AC suy ra 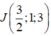 và (Q) là mặt phẳng trung trực của đoạn AC
và (Q) là mặt phẳng trung trực của đoạn AC
Mặt phẳng (Q) đi qua J và nhận ![]() làm vec tơ pháp tuyến có phương trình là:
làm vec tơ pháp tuyến có phương trình là:
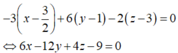
Khi đó d = (P) ∩ (Q)
Ta có d có vectơ chỉ phương ![]() và đi qua M là nghiệm của hệ
và đi qua M là nghiệm của hệ 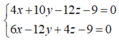 , ta chọn x = 4 suy ra y = 2 và z = 9/4. Vậy
, ta chọn x = 4 suy ra y = 2 và z = 9/4. Vậy 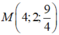
Phương trình tham số của d là: 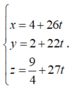


Như vậy có 4 mặt phẳng thỏa mãn yêu cầu là:
Mặt phẳng qua O và song song với mặt phẳng (ABC)
Mặt phẳng qua O và trung điểm của AB, AC
Mặt phẳng qua O và trung điểm của AB, BC
Mặt phẳng qua O và trung điểm của AC, BC. Chọn A.

Chọn A
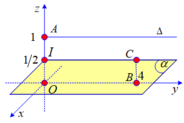
Vì đường thẳng Δ đi qua điểm A (0;0;1) và vuông góc với mặt phẳng Ozx thì Δ song song với trục Oy và nằm trong mặt phẳng Oyz. Dễ thấy OA là đường vuông góc chung của Δ và Ox
Xét mặt phẳng (α) đi qua I (0;0;1/2) và là mặt phẳng trung trực của OA.
Khi đó Δ // (α), Ox // (α) và mọi điểm nằm trên (α) có khoảng cách đến Δ và Ox là bằng nhau.
Vậy tập hợp điểm C là các điểm cách đều đường thẳng Δ và trục Ox là mặt phẳng (α). Mặt phẳng (α) đi qua I (0;0;1/2) có véc tơ pháp tuyến là ![]() nên có phương trình:
nên có phương trình: 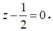
Đoạn BC nhỏ nhất khi C là hình chiếu vuông góc của B lên (α). Do đó khoảng cách nhỏ nhất giữa điểm B (0;4;0) tới điểm C chính là khoảng cách từ B (0;4;0) đến mặt phẳng (α):
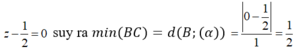
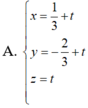
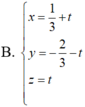
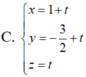
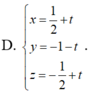




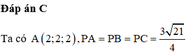
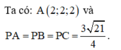
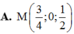

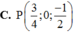
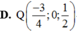
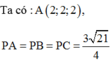
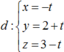 .Tọa độ giao điểm của mặt phẳng (ABC) và đường thẳng d là
.Tọa độ giao điểm của mặt phẳng (ABC) và đường thẳng d là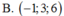
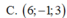

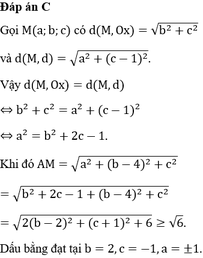
Có 2 cách hiểu:
- Đường thẳng mà mọi điểm trên nó cách đều 3 điểm A;B;C thì chỉ có 1, là đường thẳng qua tâm đường tròn ngoại tiếp và vuông góc mặt phẳng (ABC)
- Đường thẳng mà khoảng cách từ 3 điểm A;B;C tới nó bằng nhau thì có 4 đường (1 đường ở câu a, và 3 đường trung bình của tam giác ABC nữa)