Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác 2AD<AB+BC+CA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì DE//AB => \(\widehat{BAD}\) = \(\widehat{ADE}\) (so le trong ) (1)
Vì AD là tia phân giác \(\widehat{BAC}\)
=> \(\widehat{BAD}\) = \(\widehat{DAC}\) = \(\frac{1}{2}\) \(\widehat{BAC}\) (2)
Từ(1) và (2) => \(\widehat{ADE}\) = \(\widehat{DAC}\) hay \(\widehat{ADE}\) = \(\widehat{DAE}\)
Trong \(\Delta\)AED có \(\widehat{ADE}\) = \(\widehat{DAE}\) nên \(\Delta\)AED là tam giác cân tại E

Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC

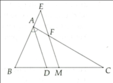

2AD<AB+BC+CA
2AD bé thua AB+BC+CA