1cho ba điểm A(5:-2:0),B(-2:3:0) và C(0;2;3). Diện tích tam giác là
2 trong khong gian hệ tọa độ oxyz cho \(\overline{u}\left(1;0;2\right),\overline{v}\left(0;1;-2\right)\) . Tích vô hướng của \(\overline{u}\) và là
3 tìm trên trục tung tất cả các điểm các đều hai điểm A(1;-3-7) và B (5;7;-5)
4 trong không gain oxyz cho điểm I (1;1;-1) và mặt phẳng (P) :2x-3y+z+5=0 . Phương trình của mặt cầu tâm I và tiếp xúc với mp (p) là
5 trong hệ tọa độ...
Đọc tiếp
1cho ba điểm A(5:-2:0),B(-2:3:0) và C(0;2;3). Diện tích tam giác là
2 trong khong gian hệ tọa độ oxyz cho \(\overline{u}\left(1;0;2\right),\overline{v}\left(0;1;-2\right)\) . Tích vô hướng của \(\overline{u}\) và là
3 tìm trên trục tung tất cả các điểm các đều hai điểm A(1;-3-7) và B (5;7;-5)
4 trong không gain oxyz cho điểm I (1;1;-1) và mặt phẳng (P) :2x-3y+z+5=0 . Phương trình của mặt cầu tâm I và tiếp xúc với mp (p) là
5 trong hệ tọa độ OXYZ , viết pt mặt cầu tâm I(2;4;-1) và qua A(5;2;3)
6 thể tích khối câu pt (x-1)^2+(y-2)^2 +(z-3)^2=4 là
7 tìm tọa độ tâm I và kính R của mặt cầu(s) :x^2+y^2+z^2-8z+10y-6z+49=0
8 pt mặt phẳng đi qua A(1;2;4) Va nhận \(\overline{n}\) =(2;3;5) la vecto pháp tuyến là
giúp mình vói nha
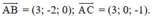
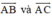là hai vec tơ chỉ phương
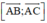= ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.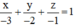
6.
Mặt cầu bán kính \(R=2\)
Thể tích: \(V=\frac{4}{3}\pi R^3=\frac{32\pi}{3}\)
7.
Chắc bạn ghi nhầm, pt có lý là: \(x^2+y^2+z^2-8x+10y-6z+49=0\)
Tọa độ tâm \(I\left(4;-5;3\right)\)
Bán kính: \(R=\sqrt{4^2+5^2+3^2-49}=1\)
8.
Phương trình mặt phẳng:
\(2\left(x-1\right)+3\left(y-2\right)+5\left(z-4\right)=0\)
\(\Leftrightarrow2x+3y+5z-28=0\)
1.
\(\overrightarrow{AB}=\left(-7;5;0\right)\) ; \(\overrightarrow{AC}=\left(-5;4;3\right)\)
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(15;21;-3\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=\sqrt{15^2+21^2+3^2}=\frac{15\sqrt{3}}{2}\)
2.
\(\overrightarrow{u}.\overrightarrow{v}=1.0+0.1+2.\left(-2\right)=-4\)
3.
Gọi \(M\left(0;m;0\right)\) là điểm thuộc trục tung
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+3;7\right)\\\overrightarrow{BM}=\left(-5;m-7;5\right)\end{matrix}\right.\)
\(AM=BM\Leftrightarrow1^2+\left(m+3\right)^2+7^2=5^2+\left(m-7\right)^2+5^2\)
\(\Leftrightarrow6m+59=-14m+99\Rightarrow m=2\Rightarrow M\left(0;2;0\right)\)
4.
\(R=d\left(I;\left(P\right)\right)=\frac{\left|2-3-1+5\right|}{\sqrt{2^2+3^2+1^2}}=\frac{3}{\sqrt{14}}\)
Phương trình đường tròn: \(\left(x-1\right)^2+\left(y-1\right)^2+\left(z+1\right)^2=\frac{9}{14}\)
5.
\(\overrightarrow{IA}=\left(3;-2;4\right)\Rightarrow R=IA=\sqrt{3^2+2^2+4^2}=\sqrt{29}\)
Pt mặt cầu: \(\left(x-2\right)^2+\left(y-4\right)^2+\left(z+1\right)^2=29\)