b, c tương tự

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có

góc BAE chung

Do đó: ΔABE\(\sim\)ΔACF

Suy ra: AB/AC=AE/AF

hay \(AB\cdot AF=AC\cdot AE\)

b: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có

góc DBH chung

Do đó: ΔBDH\(\sim\)ΔBEC
Suy ra: BD/BE=BH/BC

hay \(BD\cdot BC=BH\cdot BE\)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F cóc

góc EAB chung

Do đó:ΔAEB\(\sim\)ΔAFC

Suy ra: AE/AF=AB/AC

hay \(AE\cdot AC=AF\cdot AB\)

b: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có

góc HBD chung

Do đó:ΔBDH\(\sim\)ΔBEC

Suy ra: BD/BE=BH/BC

hay \(BD\cdot BC=BH\cdot BE\)

Xét ΔHFB vuông tại F và ΔHEC vuông tại E có

\(\widehat{FHB}=\widehat{EHC}\)

Do đó: ΔFHB\(\sim\)ΔEHC

Xét ΔBDH vuông tại D và ΔBEC vuông tại E có

\(\widehat{DBH}\) chung

Do đó: ΔBDH\(\sim\)ΔBEC
Suy ra: BD/BE=BH/BC

hay \(BD\cdot BC=BE\cdot BH\)

Xét ΔCDH vuông tại D và ΔCFB vuông tại F có

\(\widehat{DCH}\) chung

Do đó: ΔCDH~ΔCFB

=>\(\dfrac{CD}{CF}=\dfrac{CH}{CB}\)

=>\(CD\cdot CB=CH\cdot CF\)

\(BH\cdot BE+CH\cdot CF\)

\(=BD\cdot BC+CD\cdot BC=BC\left(BD+CD\right)=BC^2\)

c) Xét ΔAEH và ΔADC có:

∠(AEH) = ∠(ADC) =  90 0

∠(DAC) là góc chung

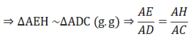
⇒ AE.AC = AD.AH

Xét Δ BEC và ΔADC có:

∠(BEC) = ∠(ADC) = 90 0

∠(ACD) là góc chung

⇒ ΔBEC ∼ ΔADC (g.g)

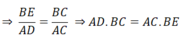
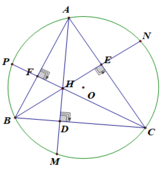
Mình làm câu cuối nhá bài này dễ ợt ý mà

Gọi góc BAC = ♪ ( cho sinh độg) =))

Thì góc BHC = 180 – ♪

Vì D là trung điểm MH => ∆ CMH cân

=> ∆ CMB = ∆ CHB (c.c.c)

=> Góc CMB bằng góc CHB = 180 – ♪

Mà A,H,D thẳng hàng và H Đối xứng với M qua trục BC

Đến đây đủ để kết luận là

Đường tròn ở sẽ đối xứng với đường tròn ngoại tiếp ∆ BHC

Nên (O) =(I)

= 2πR

Với I là tâm